
Question Number 153950 by liberty last updated on 12/Sep/21

Answered by EDWIN88 last updated on 13/Sep/21
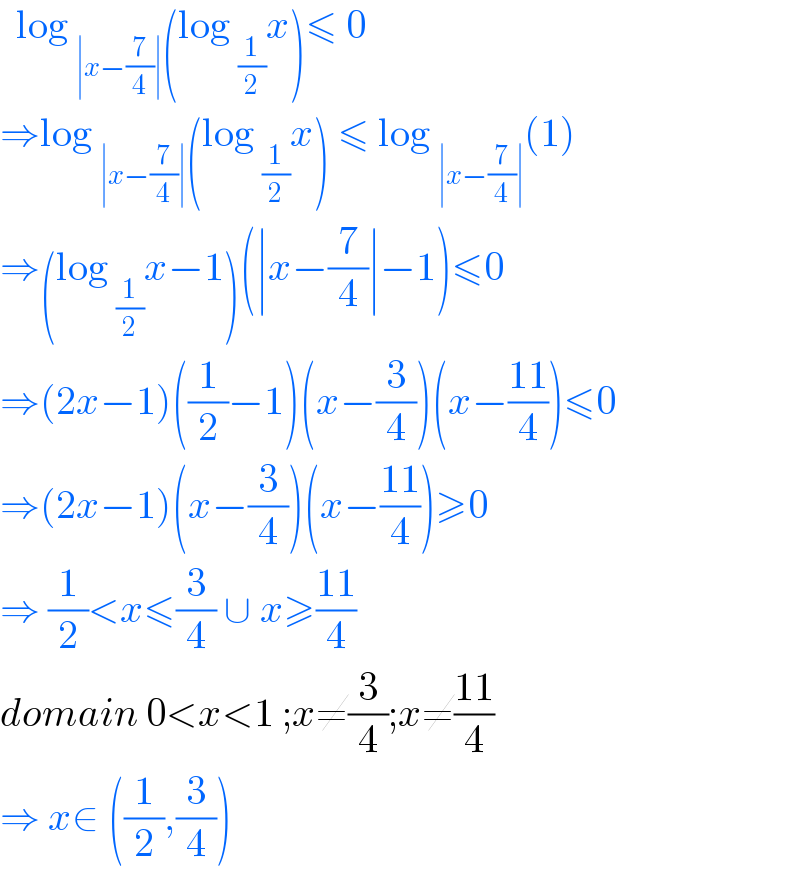
$$\:\:\mathrm{log}\:_{\mid{x}−\frac{\mathrm{7}}{\mathrm{4}}\mid} \left(\mathrm{log}\:_{\frac{\mathrm{1}}{\mathrm{2}}} {x}\right)\leqslant\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{log}\:_{\mid{x}−\frac{\mathrm{7}}{\mathrm{4}}\mid} \left(\mathrm{log}\:_{\frac{\mathrm{1}}{\mathrm{2}}} {x}\right)\:\leqslant\:\mathrm{log}\:_{\mid{x}−\frac{\mathrm{7}}{\mathrm{4}}\mid} \left(\mathrm{1}\right) \\ $$$$\Rightarrow\left(\mathrm{log}\:_{\frac{\mathrm{1}}{\mathrm{2}}} {x}−\mathrm{1}\right)\left(\mid{x}−\frac{\mathrm{7}}{\mathrm{4}}\mid−\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right)\left({x}−\frac{\mathrm{11}}{\mathrm{4}}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right)\left({x}−\frac{\mathrm{11}}{\mathrm{4}}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}<{x}\leqslant\frac{\mathrm{3}}{\mathrm{4}}\:\cup\:{x}\geqslant\frac{\mathrm{11}}{\mathrm{4}}\: \\ $$$${domain}\:\mathrm{0}<{x}<\mathrm{1}\:;{x}\neq\frac{\mathrm{3}}{\mathrm{4}};{x}\neq\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$\Rightarrow\:{x}\in\:\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{4}}\right)\: \\ $$
