
Question Number 153949 by talminator2856791 last updated on 12/Sep/21
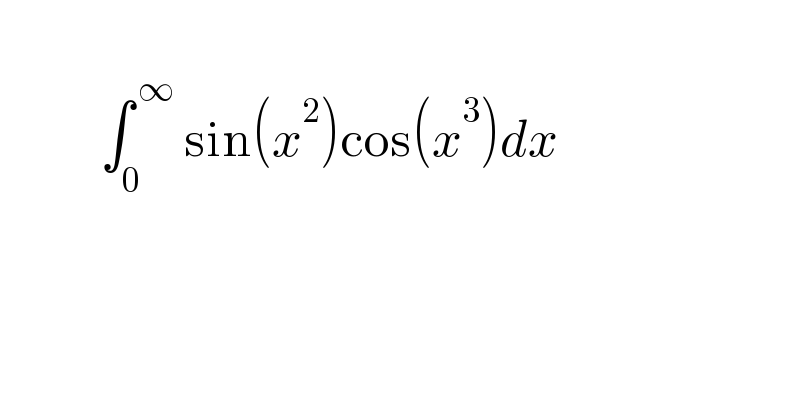
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\mathrm{sin}\left({x}^{\mathrm{2}} \right)\mathrm{cos}\left({x}^{\mathrm{3}} \right){dx} \\ $$$$\: \\ $$
Answered by mindispower last updated on 16/Sep/21
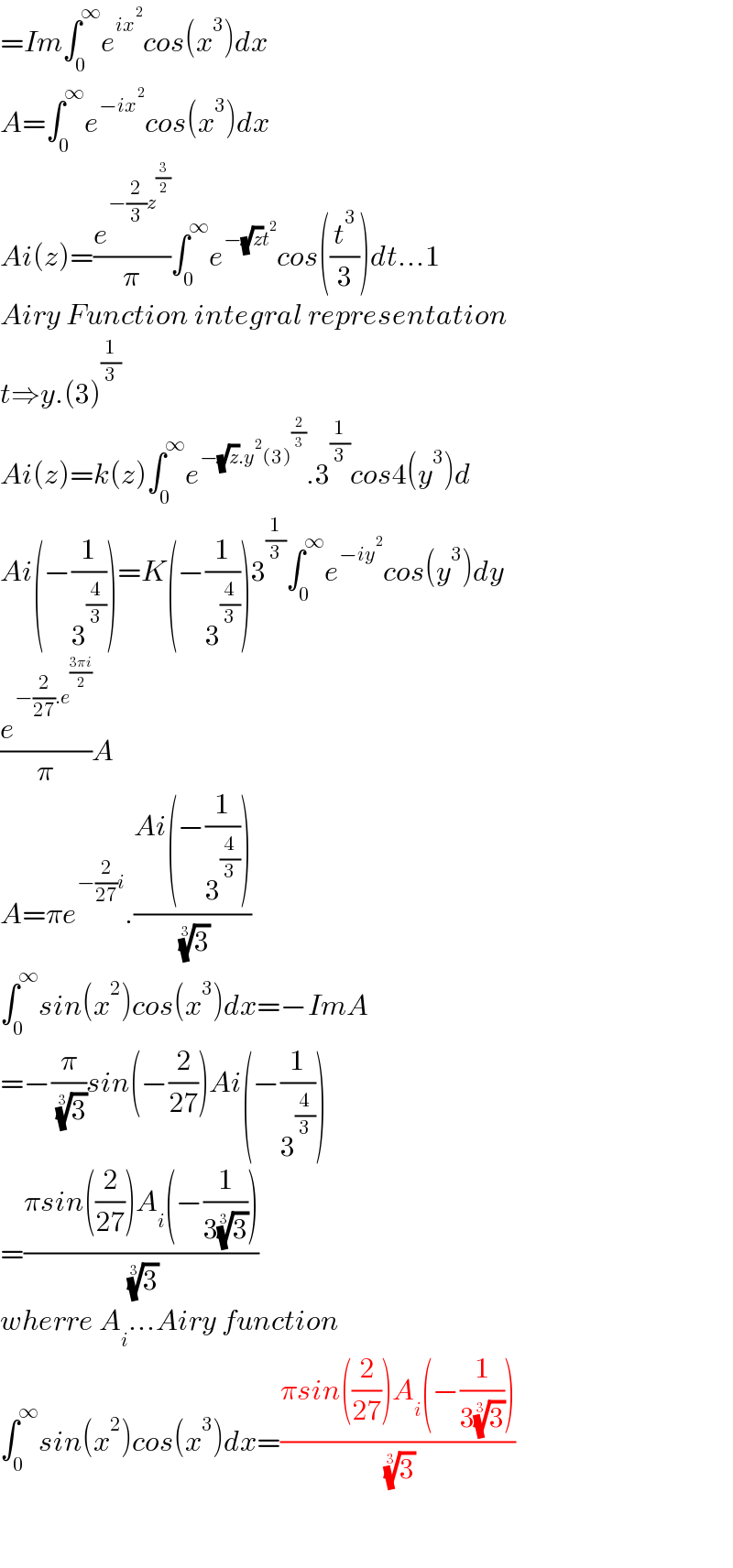
$$={Im}\int_{\mathrm{0}} ^{\infty} {e}^{{ix}^{\mathrm{2}} } {cos}\left({x}^{\mathrm{3}} \right){dx} \\ $$$${A}=\int_{\mathrm{0}} ^{\infty} {e}^{−{ix}^{\mathrm{2}} } {cos}\left({x}^{\mathrm{3}} \right){dx} \\ $$$${Ai}\left({z}\right)=\frac{{e}^{−\frac{\mathrm{2}}{\mathrm{3}}{z}^{\frac{\mathrm{3}}{\mathrm{2}}} } }{\pi}\int_{\mathrm{0}} ^{\infty} {e}^{−\sqrt{{z}}{t}^{\mathrm{2}} } {cos}\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right){dt}...\mathrm{1} \\ $$$${Airy}\:{Function}\:{integral}\:{representation} \\ $$$${t}\Rightarrow{y}.\left(\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${Ai}\left({z}\right)={k}\left({z}\right)\int_{\mathrm{0}} ^{\infty} {e}^{−\sqrt{{z}}.{y}^{\mathrm{2}} \left(\mathrm{3}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} } .\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} {cos}\mathrm{4}\left({y}^{\mathrm{3}} \right){d} \\ $$$${Ai}\left(−\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{4}}{\mathrm{3}}} }\right)={K}\left(−\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{4}}{\mathrm{3}}} }\right)\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \int_{\mathrm{0}} ^{\infty} {e}^{−{iy}^{\mathrm{2}} } {cos}\left({y}^{\mathrm{3}} \right){dy} \\ $$$$\frac{{e}^{−\frac{\mathrm{2}}{\mathrm{27}}.{e}^{\frac{\mathrm{3}\pi{i}}{\mathrm{2}}} } }{\pi}{A} \\ $$$${A}=\pi{e}^{−\frac{\mathrm{2}}{\mathrm{27}}{i}} .\frac{{Ai}\left(−\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{4}}{\mathrm{3}}} }\right)}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{\mathrm{2}} \right){cos}\left({x}^{\mathrm{3}} \right){dx}=−{ImA} \\ $$$$=−\frac{\pi}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}}{sin}\left(−\frac{\mathrm{2}}{\mathrm{27}}\right){Ai}\left(−\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{4}}{\mathrm{3}}} }\right) \\ $$$$=\frac{\pi{sin}\left(\frac{\mathrm{2}}{\mathrm{27}}\right){A}_{{i}} \left(−\frac{\mathrm{1}}{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{3}}}\right)}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}} \\ $$$${wherre}\:{A}_{{i}} ...{Airy}\:{function} \\ $$$$\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{\mathrm{2}} \right){cos}\left({x}^{\mathrm{3}} \right){dx}=\frac{\pi{sin}\left(\frac{\mathrm{2}}{\mathrm{27}}\right){A}_{{i}} \left(−\frac{\mathrm{1}}{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{3}}}\right)}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$
Commented by talminator2856791 last updated on 23/Sep/21
$$\:\mathrm{integral}\:\mathrm{master}!\:\: \\ $$
