
Question Number 153918 by joki last updated on 12/Sep/21

$$\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{an}\:\mathrm{object}\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{with} \\ $$$$\mathrm{radius}\:\mathrm{1}.\:\mathrm{suppose}\:\mathrm{that}\:\mathrm{all}\:\mathrm{section}\:\mathrm{of}\:\mathrm{the}\:\mathrm{object}\:\mathrm{are} \\ $$$$\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{a}\:\mathrm{diameter}\:\mathrm{of}\:\mathrm{a}\:\mathrm{square}.\:\mathrm{determine} \\ $$$$\mathrm{the}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{object}? \\ $$
Answered by talminator2856791 last updated on 12/Sep/21
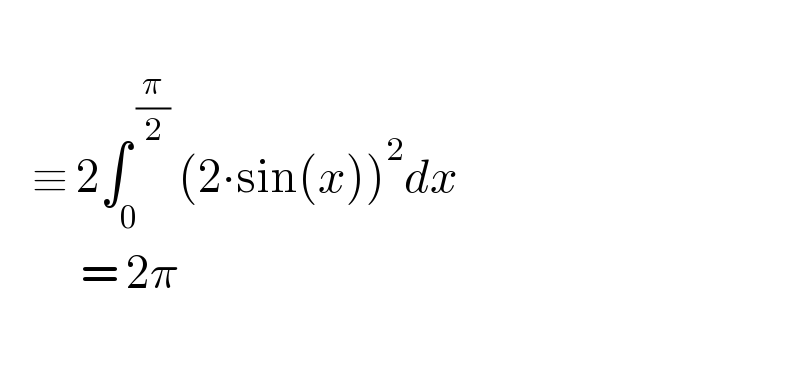
$$\: \\ $$$$\:\:\:\:\equiv\:\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{2}\centerdot\mathrm{sin}\left({x}\right)\right)^{\mathrm{2}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\pi \\ $$$$\: \\ $$
Commented by alisiao last updated on 12/Sep/21
![= (2 ∫_0 ^( (𝛑/2)) ( ((e^(ix) −e^(−ix) )/i))^2 dx) =(−2 ∫_0 ^( (𝛑/2)) ( e^(2ix) −2 +e^(−2ix) )dx) = (−2 ((e^(2ix) /(2i)) − 2x − (e^(−2ix) /(2i)))_( 0) ^( (𝛑/2)) ) =(−2( sin(2x) −2 x)_( 0) ^( (𝛑/2)) ) = [ −2(0−𝛑)] = 2𝛑 ⟨ M . T ⟩](Q153938.png)
$$=\:\:\left(\mathrm{2}\:\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \left(\:\frac{\boldsymbol{{e}}^{\boldsymbol{{ix}}} −\boldsymbol{{e}}^{−\boldsymbol{{ix}}} }{\boldsymbol{{i}}}\right)^{\mathrm{2}} \boldsymbol{{dx}}\right) \\ $$$$ \\ $$$$=\left(−\mathrm{2}\:\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \left(\:\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{ix}}} \:−\mathrm{2}\:+\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{ix}}} \right)\boldsymbol{{dx}}\right) \\ $$$$ \\ $$$$=\:\:\left(−\mathrm{2}\:\left(\frac{\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{ix}}} }{\mathrm{2}\boldsymbol{{i}}}\:−\:\mathrm{2}\boldsymbol{{x}}\:−\:\frac{\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{ix}}} }{\mathrm{2}\boldsymbol{{i}}}\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\right)}}\:\right) \\ $$$$ \\ $$$$=\left(−\mathrm{2}\left(\:\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{x}}\right)\:−\mathrm{2}\:\boldsymbol{{x}}\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\right)}}\right) \\ $$$$ \\ $$$$=\:\:\left[\:−\mathrm{2}\left(\mathrm{0}−\boldsymbol{\pi}\right)\right]\:=\:\mathrm{2}\boldsymbol{\pi} \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
Commented by alisiao last updated on 12/Sep/21
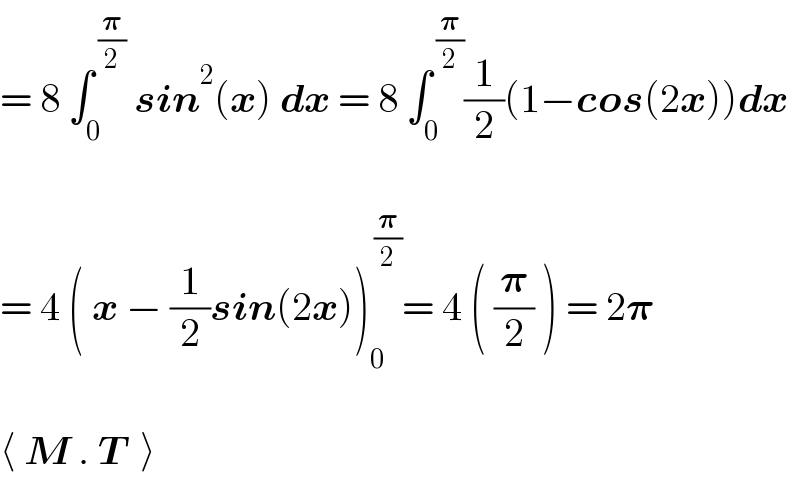
$$=\:\mathrm{8}\:\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:\boldsymbol{{sin}}^{\mathrm{2}} \left(\boldsymbol{{x}}\right)\:\boldsymbol{{dx}}\:=\:\mathrm{8}\:\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\boldsymbol{{cos}}\left(\mathrm{2}\boldsymbol{{x}}\right)\right)\boldsymbol{{dx}} \\ $$$$ \\ $$$$=\:\mathrm{4}\:\left(\:\boldsymbol{{x}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{x}}\right)\right)_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} =\:\mathrm{4}\:\left(\:\frac{\boldsymbol{\pi}}{\mathrm{2}}\:\right)\:=\:\mathrm{2}\boldsymbol{\pi} \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
