
Question Number 1539 by 314159 last updated on 17/Aug/15
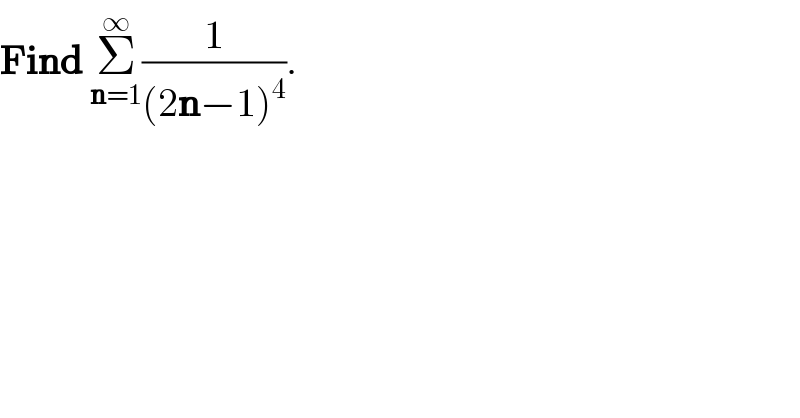
$$\boldsymbol{\mathrm{Find}}\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}\right)^{\mathrm{4}} }. \\ $$
Answered by 123456 last updated on 17/Aug/15
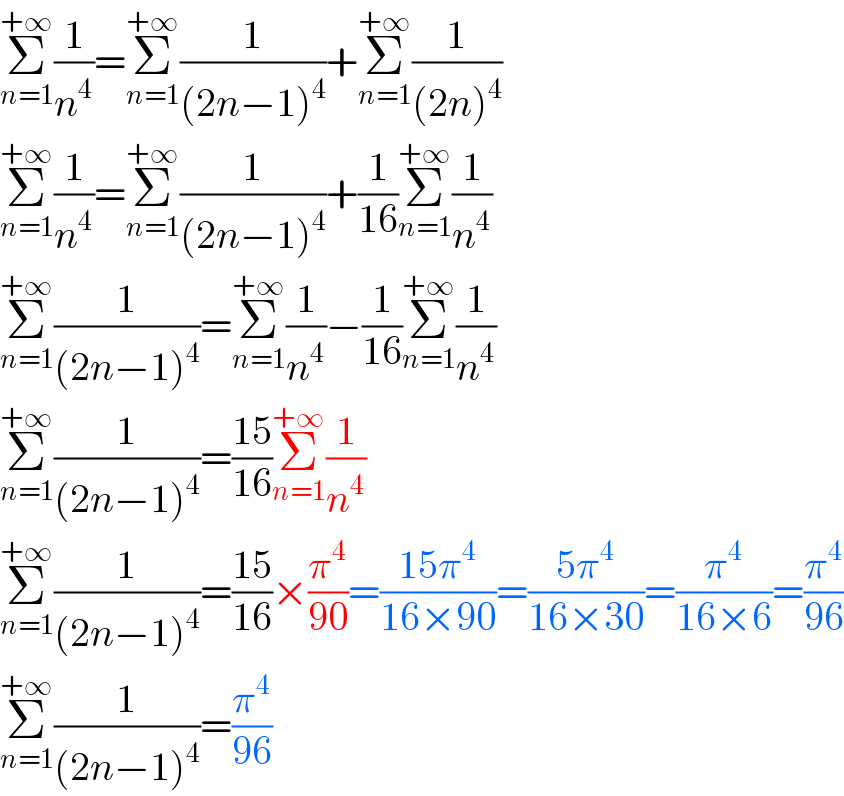
$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} }=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{4}} }+\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{4}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} }=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{16}}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{4}} }=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{16}}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{15}}{\mathrm{16}}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{15}}{\mathrm{16}}×\frac{\pi^{\mathrm{4}} }{\mathrm{90}}=\frac{\mathrm{15}\pi^{\mathrm{4}} }{\mathrm{16}×\mathrm{90}}=\frac{\mathrm{5}\pi^{\mathrm{4}} }{\mathrm{16}×\mathrm{30}}=\frac{\pi^{\mathrm{4}} }{\mathrm{16}×\mathrm{6}}=\frac{\pi^{\mathrm{4}} }{\mathrm{96}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{4}} }=\frac{\pi^{\mathrm{4}} }{\mathrm{96}} \\ $$
Commented by 314159 last updated on 17/Aug/15

$$\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{lot}}... \\ $$
Commented by 112358 last updated on 17/Aug/15
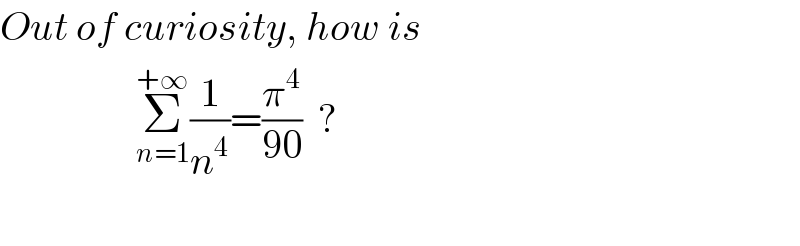
$${Out}\:{of}\:{curiosity},\:{how}\:{is} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} }=\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:\:?\: \\ $$$$ \\ $$
Commented by 123456 last updated on 17/Aug/15

$$\mathrm{rieman}\:\mathrm{zeta}\:\mathrm{function},\:\mathrm{later}\:\mathrm{i}\:\mathrm{answer}\:\mathrm{you} \\ $$
Commented by 112358 last updated on 17/Aug/15

$${Thanks}\: \\ $$
