
Question Number 153847 by mathdanisur last updated on 11/Sep/21
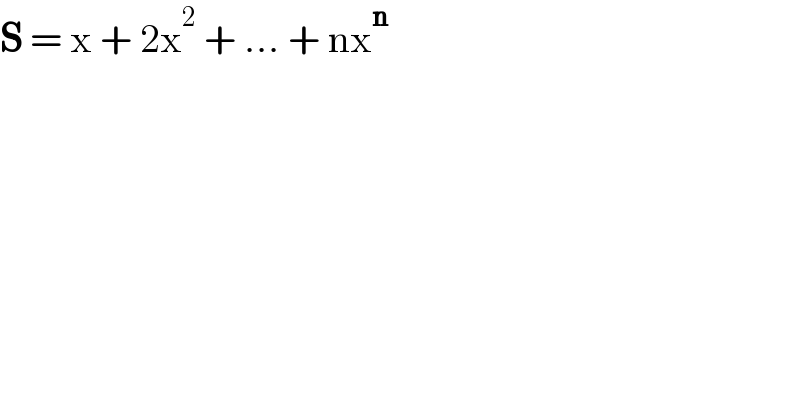
$$\boldsymbol{\mathrm{S}}\:=\:\mathrm{x}\:+\:\mathrm{2x}^{\mathrm{2}} \:+\:...\:+\:\mathrm{nx}^{\boldsymbol{\mathrm{n}}} \\ $$$$ \\ $$
Answered by liberty last updated on 11/Sep/21
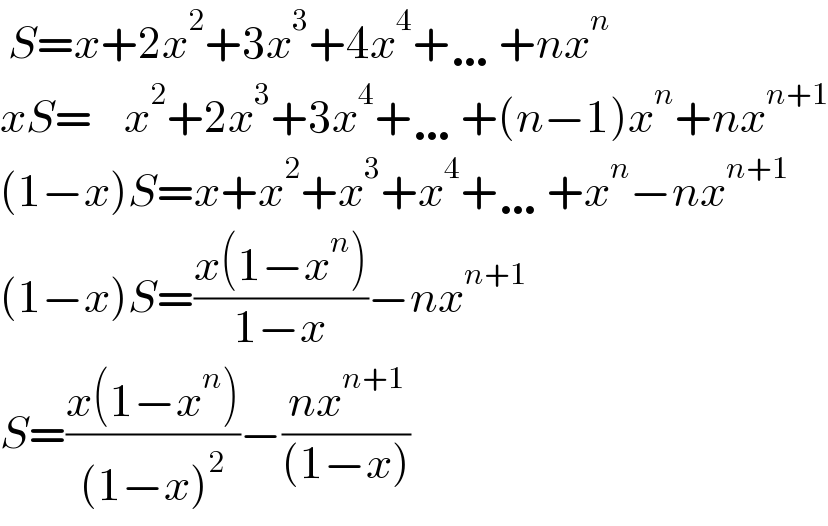
$$\:{S}={x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{4}} +\ldots+{nx}^{{n}} \\ $$$${xS}=\:\:\:\:{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{4}} +\ldots+\left({n}−\mathrm{1}\right){x}^{{n}} +{nx}^{{n}+\mathrm{1}} \\ $$$$\left(\mathrm{1}−{x}\right){S}={x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +\ldots+{x}^{{n}} −{nx}^{{n}+\mathrm{1}} \\ $$$$\left(\mathrm{1}−{x}\right){S}=\frac{{x}\left(\mathrm{1}−{x}^{{n}} \right)}{\mathrm{1}−{x}}−{nx}^{{n}+\mathrm{1}} \\ $$$${S}=\frac{{x}\left(\mathrm{1}−{x}^{{n}} \right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }−\frac{{nx}^{{n}+\mathrm{1}} }{\left(\mathrm{1}−{x}\right)} \\ $$
Commented by mathdanisur last updated on 11/Sep/21

$$\mathrm{thanks}\:\mathrm{ser}\:\mathrm{nice} \\ $$
Commented by peter frank last updated on 11/Sep/21

$$\mathrm{thanks} \\ $$
Answered by mr W last updated on 11/Sep/21
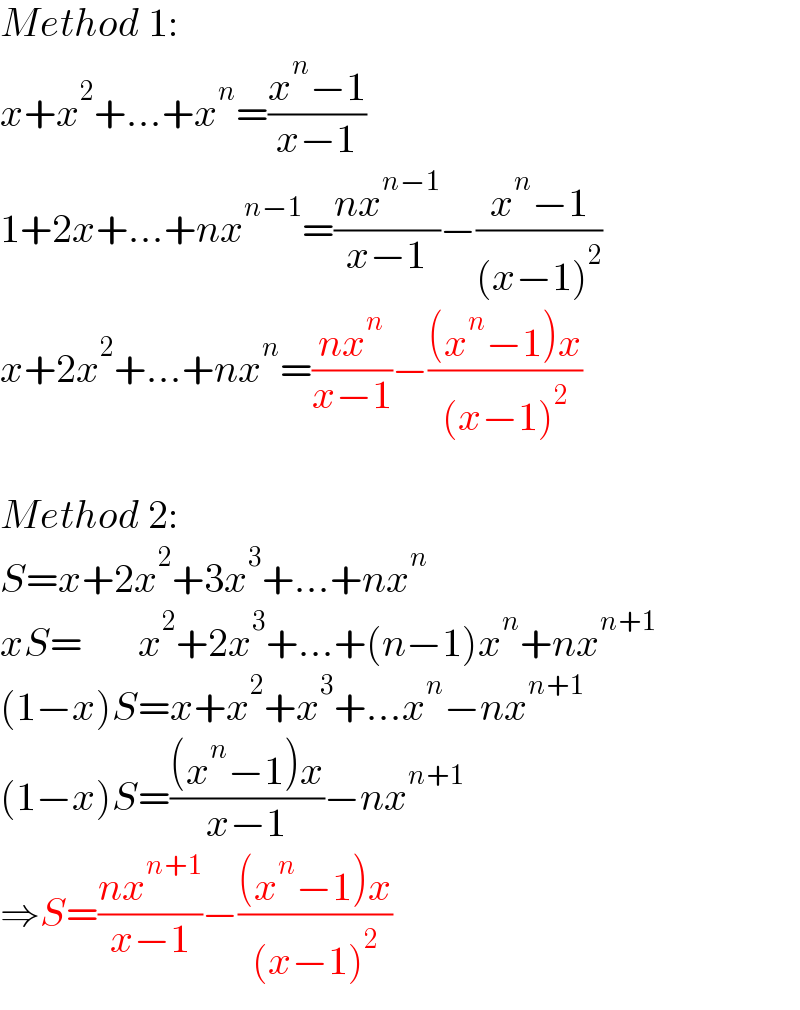
$${Method}\:\mathrm{1}: \\ $$$${x}+{x}^{\mathrm{2}} +...+{x}^{{n}} =\frac{{x}^{{n}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\mathrm{1}+\mathrm{2}{x}+...+{nx}^{{n}−\mathrm{1}} =\frac{{nx}^{{n}−\mathrm{1}} }{{x}−\mathrm{1}}−\frac{{x}^{{n}} −\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${x}+\mathrm{2}{x}^{\mathrm{2}} +...+{nx}^{{n}} =\frac{{nx}^{{n}} }{{x}−\mathrm{1}}−\frac{\left({x}^{{n}} −\mathrm{1}\right){x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${Method}\:\mathrm{2}: \\ $$$${S}={x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} +...+{nx}^{{n}} \\ $$$${xS}=\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}} +...+\left({n}−\mathrm{1}\right){x}^{{n}} +{nx}^{{n}+\mathrm{1}} \\ $$$$\left(\mathrm{1}−{x}\right){S}={x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...{x}^{{n}} −{nx}^{{n}+\mathrm{1}} \\ $$$$\left(\mathrm{1}−{x}\right){S}=\frac{\left({x}^{{n}} −\mathrm{1}\right){x}}{{x}−\mathrm{1}}−{nx}^{{n}+\mathrm{1}} \\ $$$$\Rightarrow{S}=\frac{{nx}^{{n}+\mathrm{1}} }{{x}−\mathrm{1}}−\frac{\left({x}^{{n}} −\mathrm{1}\right){x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by mathdanisur last updated on 11/Sep/21

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{thanks}\:\mathrm{ser} \\ $$
