
Question Number 153840 by liberty last updated on 11/Sep/21
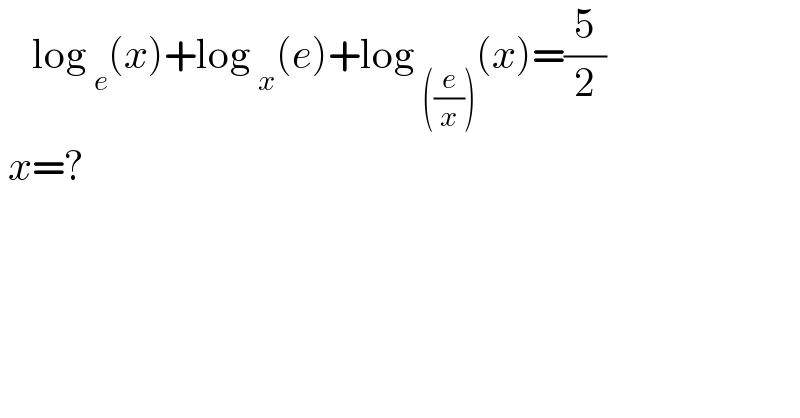
$$\:\:\:\:\mathrm{log}\:_{{e}} \left({x}\right)+\mathrm{log}\:_{{x}} \left({e}\right)+\mathrm{log}\:_{\left(\frac{{e}}{{x}}\right)} \left({x}\right)=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\:{x}=? \\ $$
Answered by Rasheed.Sindhi last updated on 11/Sep/21
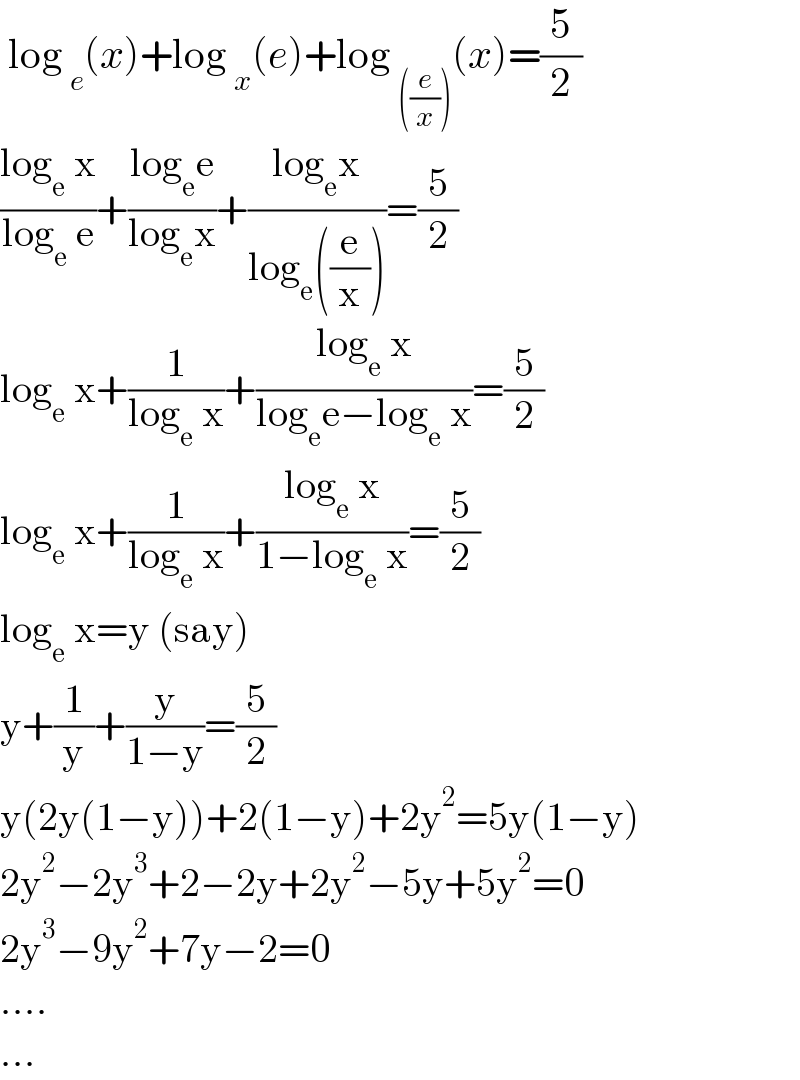
$$\:\mathrm{log}\:_{{e}} \left({x}\right)+\mathrm{log}\:_{{x}} \left({e}\right)+\mathrm{log}\:_{\left(\frac{{e}}{{x}}\right)} \left({x}\right)=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\frac{\mathrm{log}_{\mathrm{e}} \:\mathrm{x}}{\mathrm{log}_{\mathrm{e}} \:\mathrm{e}}+\frac{\mathrm{log}_{\mathrm{e}} \mathrm{e}}{\mathrm{log}_{\mathrm{e}} \mathrm{x}}+\frac{\mathrm{log}_{\mathrm{e}} \mathrm{x}}{\mathrm{log}_{\mathrm{e}} \left(\frac{\mathrm{e}}{\mathrm{x}}\right)}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{log}_{\mathrm{e}} \:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{e}} \:\mathrm{x}}+\frac{\mathrm{log}_{\mathrm{e}} \:\mathrm{x}}{\mathrm{log}_{\mathrm{e}} \mathrm{e}−\mathrm{log}_{\mathrm{e}} \:\mathrm{x}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{log}_{\mathrm{e}} \:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{e}} \:\mathrm{x}}+\frac{\mathrm{log}_{\mathrm{e}} \:\mathrm{x}}{\mathrm{1}−\mathrm{log}_{\mathrm{e}} \:\mathrm{x}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{log}_{\mathrm{e}} \:\mathrm{x}=\mathrm{y}\:\left(\mathrm{say}\right) \\ $$$$\mathrm{y}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{y}}{\mathrm{1}−\mathrm{y}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{y}\left(\mathrm{2y}\left(\mathrm{1}−\mathrm{y}\right)\right)+\mathrm{2}\left(\mathrm{1}−\mathrm{y}\right)+\mathrm{2y}^{\mathrm{2}} =\mathrm{5y}\left(\mathrm{1}−\mathrm{y}\right) \\ $$$$\mathrm{2y}^{\mathrm{2}} −\mathrm{2y}^{\mathrm{3}} +\mathrm{2}−\mathrm{2y}+\mathrm{2y}^{\mathrm{2}} −\mathrm{5y}+\mathrm{5y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2y}^{\mathrm{3}} −\mathrm{9y}^{\mathrm{2}} +\mathrm{7y}−\mathrm{2}=\mathrm{0} \\ $$$$.... \\ $$$$... \\ $$
