
Question Number 153596 by SANOGO last updated on 08/Sep/21
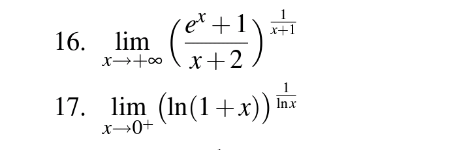
Commented by SANOGO last updated on 08/Sep/21

$${merci}\:{bien} \\ $$
Commented by SANOGO last updated on 08/Sep/21
$${merci}\:{bien} \\ $$
Commented by tabata last updated on 08/Sep/21
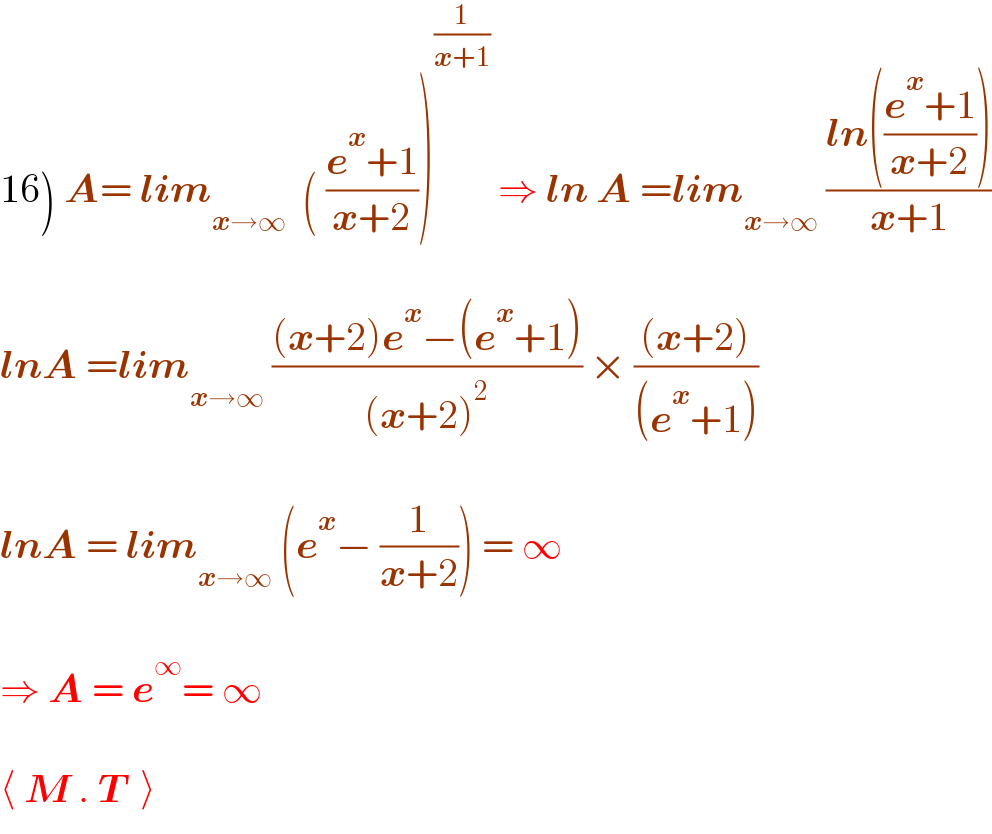
$$\left.\mathrm{16}\right)\:\boldsymbol{{A}}=\:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\infty} \:\:\left(\:\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} +\mathrm{1}}{\boldsymbol{{x}}+\mathrm{2}}\right)^{\frac{\mathrm{1}}{\boldsymbol{{x}}+\mathrm{1}}} \:\Rightarrow\:\boldsymbol{{ln}}\:\boldsymbol{{A}}\:=\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\infty} \:\frac{\boldsymbol{{ln}}\left(\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} +\mathrm{1}}{\boldsymbol{{x}}+\mathrm{2}}\right)}{\boldsymbol{{x}}+\mathrm{1}} \\ $$$$ \\ $$$$\boldsymbol{{lnA}}\:=\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\infty} \:\frac{\left(\boldsymbol{{x}}+\mathrm{2}\right)\boldsymbol{{e}}^{\boldsymbol{{x}}} −\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} +\mathrm{1}\right)}{\left(\boldsymbol{{x}}+\mathrm{2}\right)^{\mathrm{2}} }\:×\:\frac{\left(\boldsymbol{{x}}+\mathrm{2}\right)}{\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} +\mathrm{1}\right)} \\ $$$$ \\ $$$$\boldsymbol{{lnA}}\:=\:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\infty} \:\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} −\:\frac{\mathrm{1}}{\boldsymbol{{x}}+\mathrm{2}}\right)\:=\:\infty\: \\ $$$$ \\ $$$$\Rightarrow\:\boldsymbol{{A}}\:=\:\boldsymbol{{e}}^{\infty} =\:\infty \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
Commented by tabata last updated on 08/Sep/21
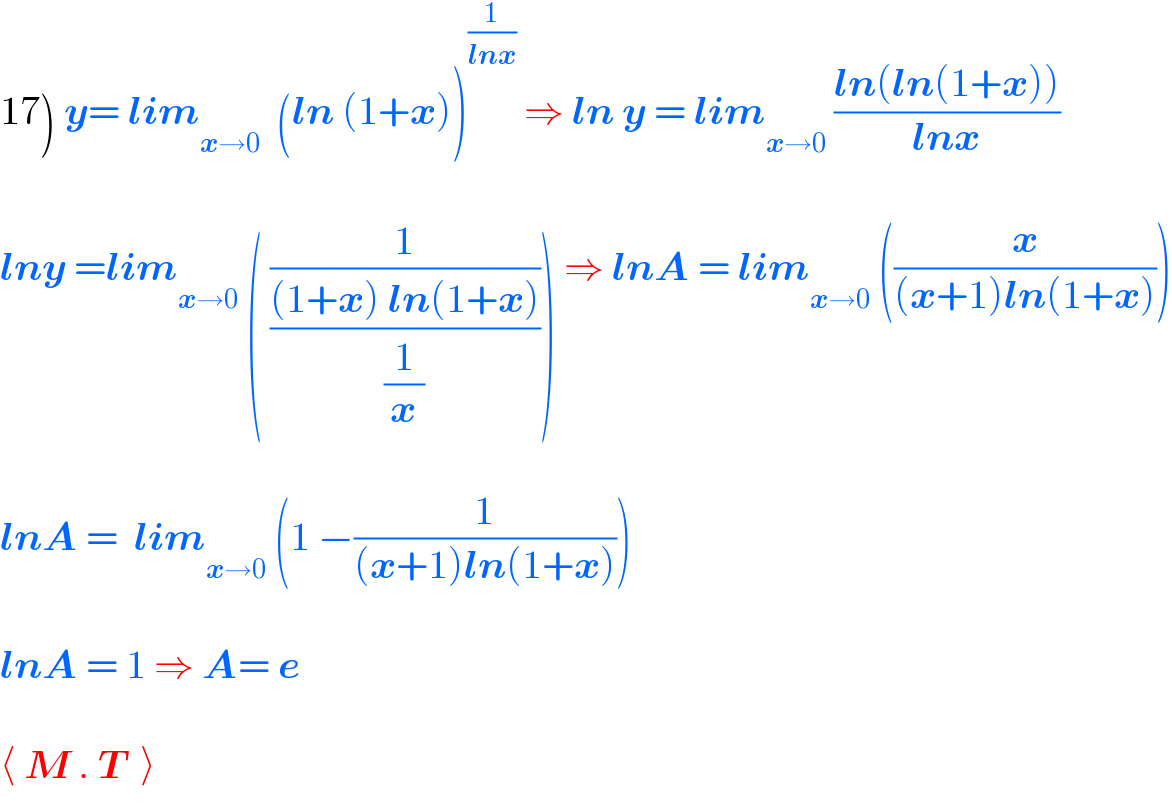
$$\left.\mathrm{17}\right)\:\boldsymbol{{y}}=\:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\mathrm{0}} \:\:\left(\boldsymbol{{ln}}\:\left(\mathrm{1}+\boldsymbol{{x}}\right)\right)^{\frac{\mathrm{1}}{\boldsymbol{{lnx}}}} \:\Rightarrow\:\boldsymbol{{ln}}\:\boldsymbol{{y}}\:=\:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\mathrm{0}} \:\frac{\boldsymbol{{ln}}\left(\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{x}}\right)\right)}{\boldsymbol{{lnx}}} \\ $$$$ \\ $$$$\boldsymbol{{lny}}\:=\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\mathrm{0}} \:\left(\:\frac{\mathrm{1}}{\frac{\left(\mathrm{1}+\boldsymbol{{x}}\right)\:\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{x}}\right)}{\frac{\mathrm{1}}{\boldsymbol{{x}}}}}\right)\:\Rightarrow\:\boldsymbol{{lnA}}\:=\:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\mathrm{0}} \:\left(\frac{\boldsymbol{{x}}}{\left(\boldsymbol{{x}}+\mathrm{1}\right)\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{x}}\right)}\right) \\ $$$$ \\ $$$$\boldsymbol{{lnA}}\:=\:\:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\mathrm{0}} \:\left(\mathrm{1}\:−\frac{\mathrm{1}}{\left(\boldsymbol{{x}}+\mathrm{1}\right)\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{x}}\right)}\right) \\ $$$$ \\ $$$$\boldsymbol{{lnA}}\:=\:\mathrm{1}\:\Rightarrow\:\boldsymbol{{A}}=\:\boldsymbol{{e}} \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
Commented by tabata last updated on 10/Sep/21
$$\boldsymbol{{you}}\:\boldsymbol{{are}}\:\boldsymbol{{welcome}} \\ $$
