
Question Number 153583 by pete last updated on 08/Sep/21
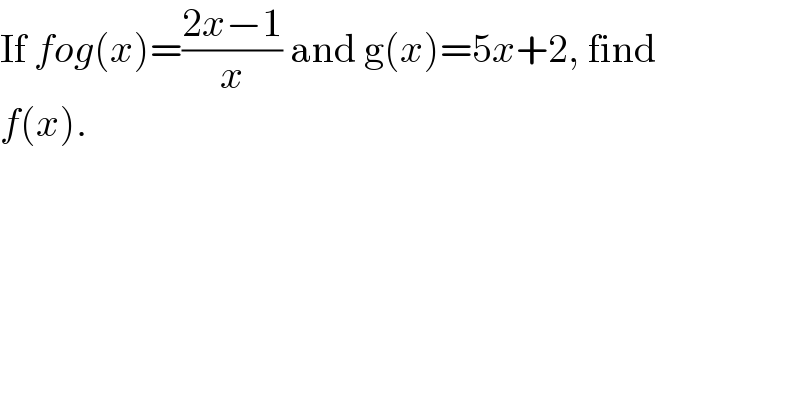
$$\mathrm{If}\:{fog}\left({x}\right)=\frac{\mathrm{2}{x}−\mathrm{1}}{{x}}\:\mathrm{and}\:\mathrm{g}\left({x}\right)=\mathrm{5}{x}+\mathrm{2},\:\mathrm{find} \\ $$$${f}\left({x}\right). \\ $$
Commented by otchereabdullai@gmail.com last updated on 08/Sep/21

$$\mathrm{nice}\:\mathrm{question} \\ $$
Commented by benhamimed last updated on 08/Sep/21
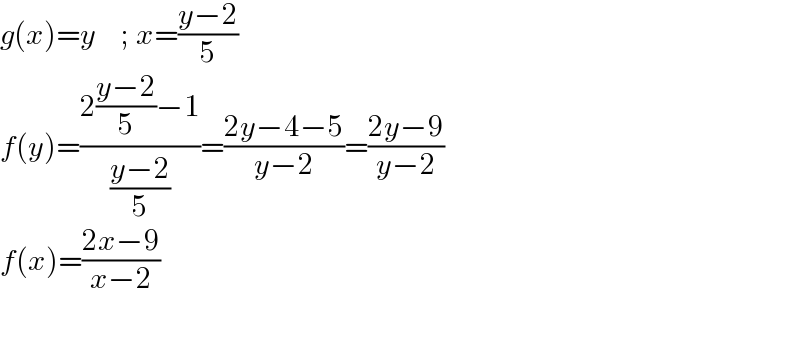
$${g}\left({x}\right)={y}\:\:\:\:;\:{x}=\frac{{y}−\mathrm{2}}{\mathrm{5}} \\ $$$${f}\left({y}\right)=\frac{\mathrm{2}\frac{{y}−\mathrm{2}}{\mathrm{5}}−\mathrm{1}}{\frac{{y}−\mathrm{2}}{\mathrm{5}}}=\frac{\mathrm{2}{y}−\mathrm{4}−\mathrm{5}}{{y}−\mathrm{2}}=\frac{\mathrm{2}{y}−\mathrm{9}}{{y}−\mathrm{2}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{x}−\mathrm{9}}{{x}−\mathrm{2}} \\ $$$$ \\ $$
Commented by pete last updated on 08/Sep/21
$$\mathrm{Thanks}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
Answered by liberty last updated on 08/Sep/21
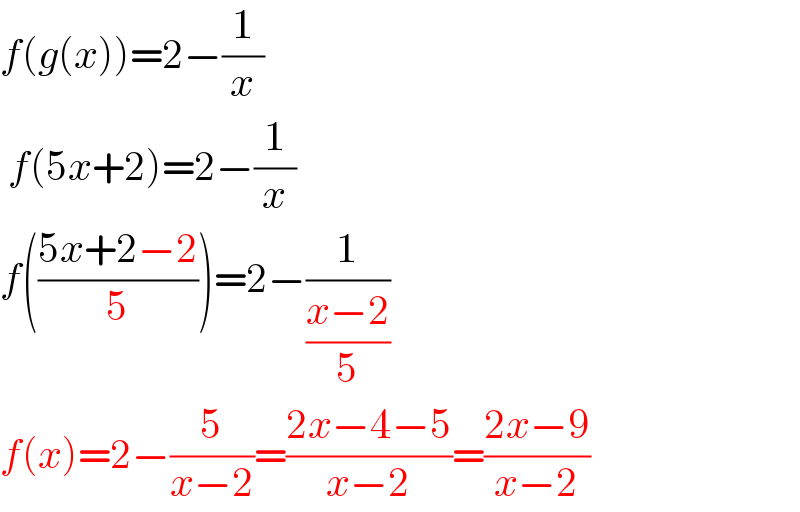
$${f}\left({g}\left({x}\right)\right)=\mathrm{2}−\frac{\mathrm{1}}{{x}} \\ $$$$\:{f}\left(\mathrm{5}{x}+\mathrm{2}\right)=\mathrm{2}−\frac{\mathrm{1}}{{x}} \\ $$$${f}\left(\frac{\mathrm{5}{x}+\mathrm{2}−\mathrm{2}}{\mathrm{5}}\right)=\mathrm{2}−\frac{\mathrm{1}}{\frac{{x}−\mathrm{2}}{\mathrm{5}}} \\ $$$${f}\left({x}\right)=\mathrm{2}−\frac{\mathrm{5}}{{x}−\mathrm{2}}=\frac{\mathrm{2}{x}−\mathrm{4}−\mathrm{5}}{{x}−\mathrm{2}}=\frac{\mathrm{2}{x}−\mathrm{9}}{{x}−\mathrm{2}} \\ $$
Commented by pete last updated on 08/Sep/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 08/Sep/21
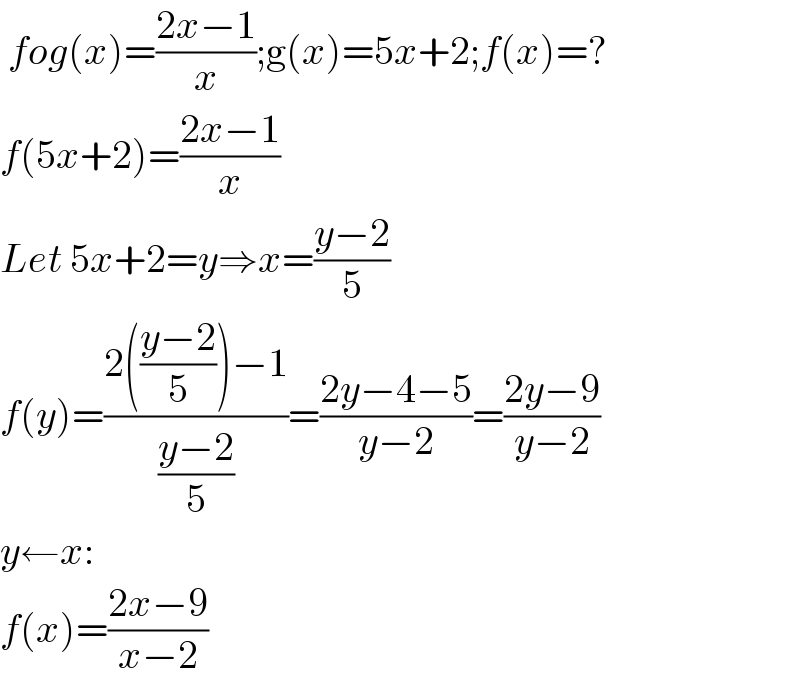
$$\:{fog}\left({x}\right)=\frac{\mathrm{2}{x}−\mathrm{1}}{{x}};\mathrm{g}\left({x}\right)=\mathrm{5}{x}+\mathrm{2};{f}\left({x}\right)=? \\ $$$${f}\left(\mathrm{5}{x}+\mathrm{2}\right)=\frac{\mathrm{2}{x}−\mathrm{1}}{{x}} \\ $$$${Let}\:\mathrm{5}{x}+\mathrm{2}={y}\Rightarrow{x}=\frac{{y}−\mathrm{2}}{\mathrm{5}} \\ $$$${f}\left({y}\right)=\frac{\mathrm{2}\left(\frac{{y}−\mathrm{2}}{\mathrm{5}}\right)−\mathrm{1}}{\frac{{y}−\mathrm{2}}{\mathrm{5}}}=\frac{\mathrm{2}{y}−\mathrm{4}−\mathrm{5}}{{y}−\mathrm{2}}=\frac{\mathrm{2}{y}−\mathrm{9}}{{y}−\mathrm{2}} \\ $$$${y}\leftarrow{x}: \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{x}−\mathrm{9}}{{x}−\mathrm{2}} \\ $$
Commented by pete last updated on 08/Sep/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by amin96 last updated on 08/Sep/21
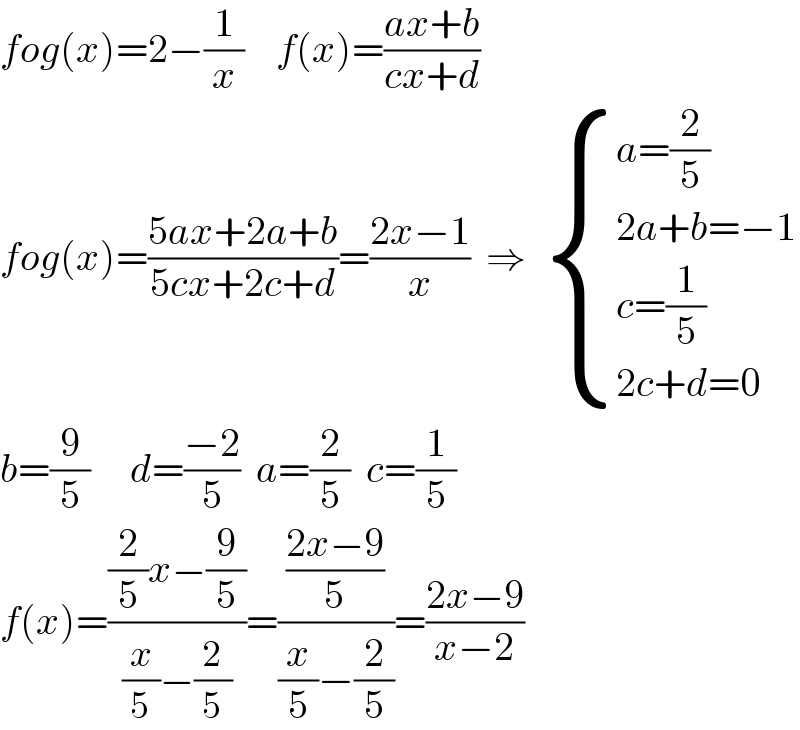
$${fog}\left({x}\right)=\mathrm{2}−\frac{\mathrm{1}}{{x}}\:\:\:\:{f}\left({x}\right)=\frac{{ax}+{b}}{{cx}+{d}} \\ $$$${fog}\left({x}\right)=\frac{\mathrm{5}{ax}+\mathrm{2}{a}+{b}}{\mathrm{5}{cx}+\mathrm{2}{c}+{d}}=\frac{\mathrm{2}{x}−\mathrm{1}}{{x}}\:\:\Rightarrow\:\:\begin{cases}{{a}=\frac{\mathrm{2}}{\mathrm{5}}}\\{\mathrm{2}{a}+{b}=−\mathrm{1}}\\{{c}=\frac{\mathrm{1}}{\mathrm{5}}}\\{\mathrm{2}{c}+{d}=\mathrm{0}}\end{cases} \\ $$$${b}=\frac{\mathrm{9}}{\mathrm{5}}\:\:\:\:\:{d}=\frac{−\mathrm{2}}{\mathrm{5}}\:\:{a}=\frac{\mathrm{2}}{\mathrm{5}}\:\:{c}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${f}\left({x}\right)=\frac{\frac{\mathrm{2}}{\mathrm{5}}{x}−\frac{\mathrm{9}}{\mathrm{5}}}{\frac{{x}}{\mathrm{5}}−\frac{\mathrm{2}}{\mathrm{5}}}=\frac{\frac{\mathrm{2}{x}−\mathrm{9}}{\mathrm{5}}}{\frac{{x}}{\mathrm{5}}−\frac{\mathrm{2}}{\mathrm{5}}}=\frac{\mathrm{2}{x}−\mathrm{9}}{{x}−\mathrm{2}} \\ $$
Answered by amin96 last updated on 08/Sep/21
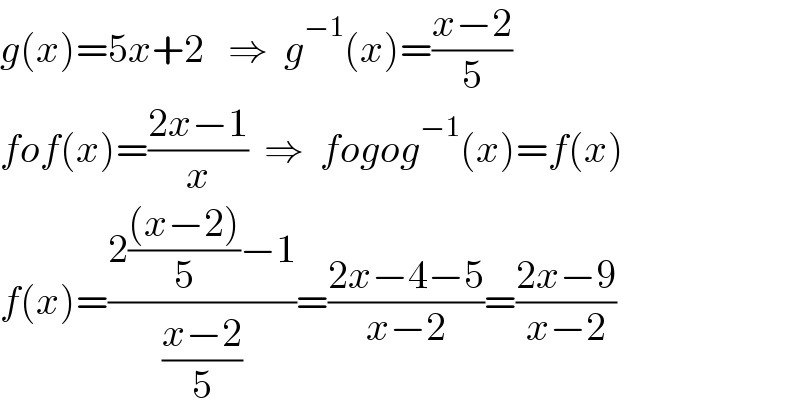
$${g}\left({x}\right)=\mathrm{5}{x}+\mathrm{2}\:\:\:\Rightarrow\:\:{g}^{−\mathrm{1}} \left({x}\right)=\frac{{x}−\mathrm{2}}{\mathrm{5}} \\ $$$${fof}\left({x}\right)=\frac{\mathrm{2}{x}−\mathrm{1}}{{x}}\:\:\Rightarrow\:\:{fogog}^{−\mathrm{1}} \left({x}\right)={f}\left({x}\right) \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}\frac{\left({x}−\mathrm{2}\right)}{\mathrm{5}}−\mathrm{1}}{\frac{{x}−\mathrm{2}}{\mathrm{5}}}=\frac{\mathrm{2}{x}−\mathrm{4}−\mathrm{5}}{{x}−\mathrm{2}}=\frac{\mathrm{2}{x}−\mathrm{9}}{{x}−\mathrm{2}} \\ $$
