
Previous in Differential Equation Next in Differential Equation
Question Number 153542 by EDWIN88 last updated on 08/Sep/21

$$\:{y}'''+{y}'=\mathrm{sec}\:{x}\: \\ $$
Answered by puissant last updated on 08/Sep/21
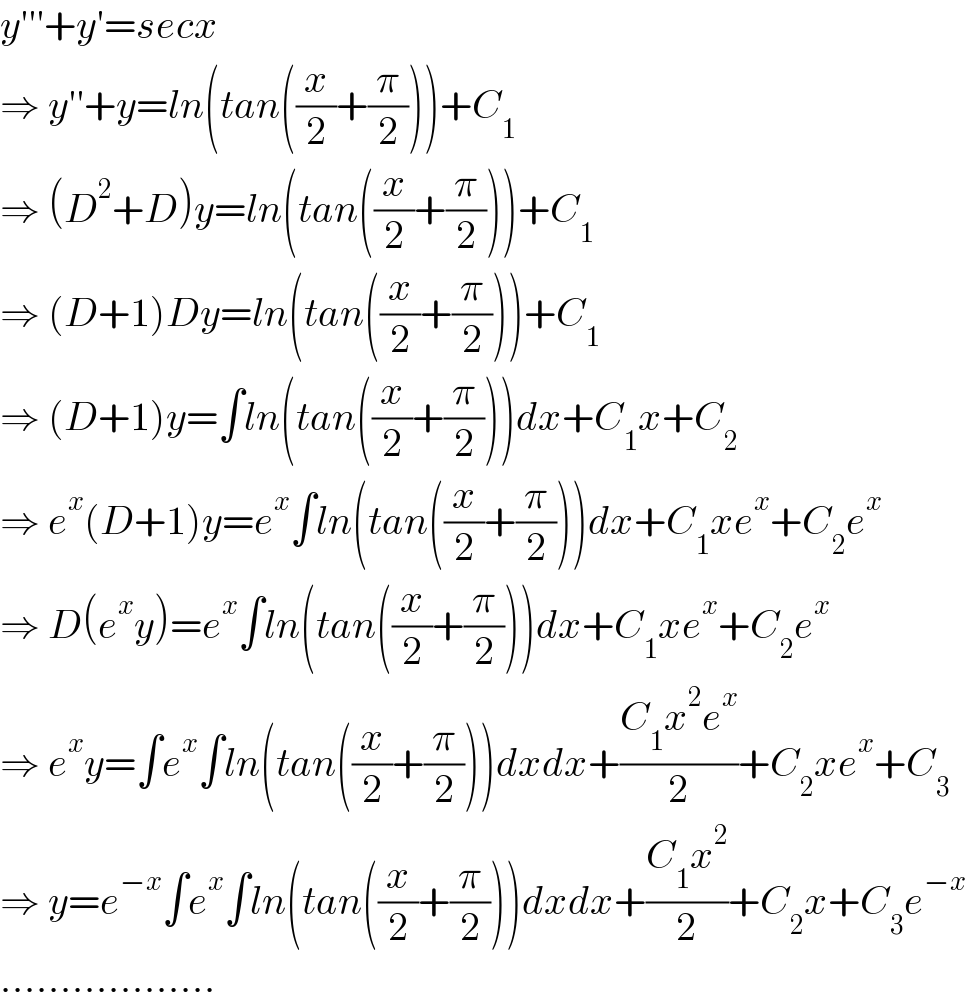
$${y}'''+{y}'={secx} \\ $$$$\Rightarrow\:{y}''+{y}={ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right)+{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:\left({D}^{\mathrm{2}} +{D}\right){y}={ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right)+{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:\left({D}+\mathrm{1}\right){Dy}={ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right)+{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:\left({D}+\mathrm{1}\right){y}=\int{ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right){dx}+{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow\:{e}^{{x}} \left({D}+\mathrm{1}\right){y}={e}^{{x}} \int{ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right){dx}+{C}_{\mathrm{1}} {xe}^{{x}} +{C}_{\mathrm{2}} {e}^{{x}} \\ $$$$\Rightarrow\:{D}\left({e}^{{x}} {y}\right)={e}^{{x}} \int{ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right){dx}+{C}_{\mathrm{1}} {xe}^{{x}} +{C}_{\mathrm{2}} {e}^{{x}} \\ $$$$\Rightarrow\:{e}^{{x}} {y}=\int{e}^{{x}} \int{ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right){dxdx}+\frac{{C}_{\mathrm{1}} {x}^{\mathrm{2}} {e}^{{x}} }{\mathrm{2}}+{C}_{\mathrm{2}} {xe}^{{x}} +{C}_{\mathrm{3}} \\ $$$$\Rightarrow\:{y}={e}^{−{x}} \int{e}^{{x}} \int{ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)\right){dxdx}+\frac{{C}_{\mathrm{1}} {x}^{\mathrm{2}} }{\mathrm{2}}+{C}_{\mathrm{2}} {x}+{C}_{\mathrm{3}} {e}^{−{x}} \\ $$$$.................. \\ $$
