
Question Number 15348 by tawa tawa last updated on 09/Jun/17
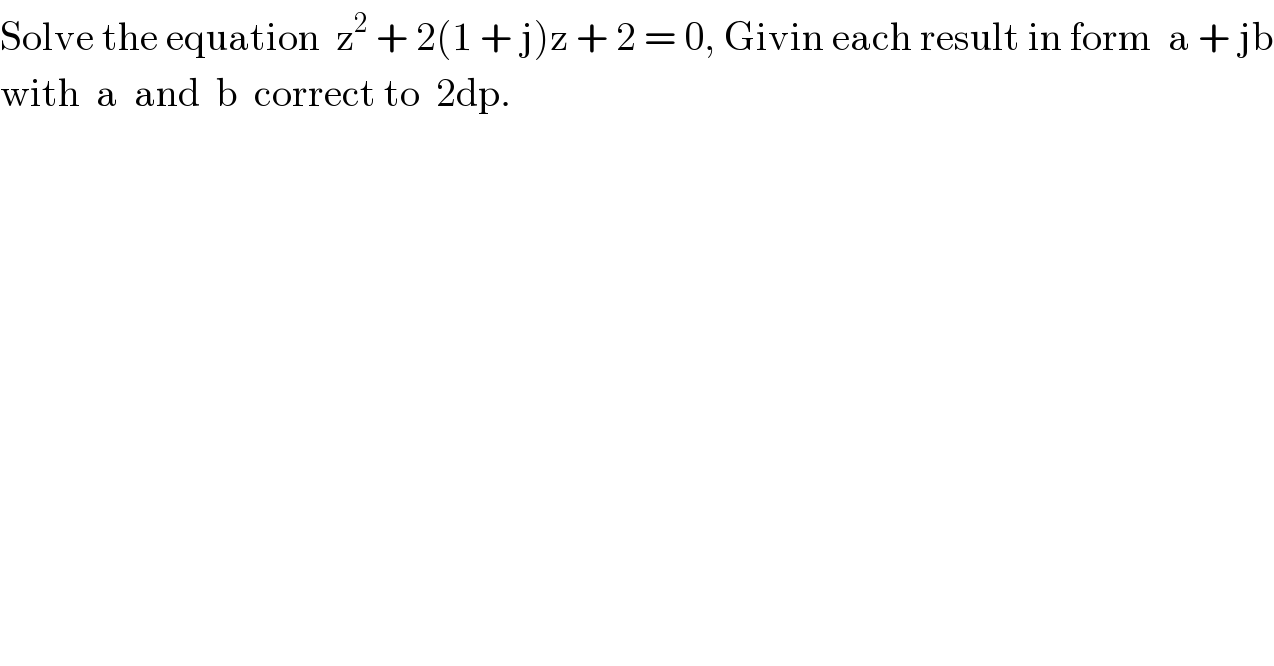
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\:\:\mathrm{z}^{\mathrm{2}} \:+\:\mathrm{2}\left(\mathrm{1}\:+\:\mathrm{j}\right)\mathrm{z}\:+\:\mathrm{2}\:=\:\mathrm{0},\:\mathrm{Givin}\:\mathrm{each}\:\mathrm{result}\:\mathrm{in}\:\mathrm{form}\:\:\mathrm{a}\:+\:\mathrm{jb} \\ $$$$\mathrm{with}\:\:\mathrm{a}\:\:\mathrm{and}\:\:\mathrm{b}\:\:\mathrm{correct}\:\mathrm{to}\:\:\mathrm{2dp}. \\ $$
Answered by RasheedSoomro last updated on 10/Jun/17

$$\mathrm{Let}\:\mathrm{z}=\mathrm{x}+\mathrm{jy} \\ $$$$\:\mathrm{z}^{\mathrm{2}} \:+\:\mathrm{2}\left(\mathrm{1}\:+\:\mathrm{j}\right)\mathrm{z}\:+\:\mathrm{2}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{jy}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+\mathrm{j}\right)\left(\mathrm{x}+\mathrm{jy}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2xyj}+\mathrm{2}\left(\mathrm{x}+\mathrm{xj}+\mathrm{yj}−\mathrm{y}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2xyj}+\mathrm{2x}+\mathrm{2xj}+\mathrm{2yj}−\mathrm{2y}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2y}+\mathrm{2}\right)+\left(\:\mathrm{2xy}+\mathrm{2x}+\mathrm{2y}\right)\mathrm{j}=\mathrm{0}+\mathrm{0j} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2y}+\mathrm{2}=\mathrm{0}\:\wedge\:\mathrm{2xy}+\mathrm{2x}+\mathrm{2y}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{2}\left(\mathrm{x}−\mathrm{y}\right)+\mathrm{2}=\mathrm{0}\:\wedge\:\mathrm{x}+\mathrm{xy}+\mathrm{y}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{2}\right)+\mathrm{2}=\mathrm{0}\:\:\wedge\:\mathrm{y}=\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\left(\mathrm{x}−\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}}\right)\left(\mathrm{x}+\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}}+\mathrm{2}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{x}}{\mathrm{x}+\mathrm{1}}×\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{x}+\mathrm{2x}+\mathrm{2}}{\mathrm{x}+\mathrm{1}}+\mathrm{2}=\mathrm{0} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}}{\mathrm{x}+\mathrm{1}}×\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}{\mathrm{x}+\mathrm{1}}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\right)+\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{Let}\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}=\mathrm{t} \\ $$$$\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{2t}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{t}^{\mathrm{2}} +\mathrm{4t}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{t}=\frac{−\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{8}}}{\mathrm{2}} \\ $$$$\mathrm{t}=−\mathrm{2}\pm\sqrt{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{2x}=−\mathrm{2}+\sqrt{\mathrm{2}}\:\:\:\vee\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}=−\mathrm{2}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}−\sqrt{\mathrm{2}}\:=\mathrm{0}\:\:\vee\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}+\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}}{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.\mathrm{4}−\mathrm{8}+\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.\mathrm{4}−\mathrm{8}−\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.−\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.−\mathrm{4}−\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\mp\mathrm{2i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{\mathrm{2}} \\ $$$$\mathrm{x}=−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\:\:\:\vee\:\:\mathrm{x}=−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{−\left(−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)}{\left(−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee\:\:\:\:\:\:\:\mathrm{y}=\frac{−\left(−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)}{\left(−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{\mathrm{1}\mp\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}{−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee\:\:\:\:\:\:\:\mathrm{y}=\frac{\mathrm{1}\pm\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{\mathrm{1}\mp\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}×\frac{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}\:\:\:\vee\:\:\:\mathrm{y}=\frac{\mathrm{1}\pm\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}×\frac{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}} \\ $$$$\mathrm{y}=\frac{\left(\mathrm{1}\mp\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)\left(\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)}{\sqrt{\mathrm{2}}−\mathrm{1}\:}\:\:\vee\:\:\:\mathrm{y}=\frac{\left(\mathrm{1}\pm\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)\left(\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)}{−\left(\sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)} \\ $$$$\mathrm{y}=\frac{\left.\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\mp\sqrt{\mathrm{2}}−\mathrm{1}\:\right)}{\sqrt{\mathrm{2}}−\mathrm{1}\:}\:\:\vee\:\:\:\mathrm{y}=\frac{\left.\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}−\mathrm{i}^{\mathrm{2}} \sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)}{−\left(\sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)} \\ $$$$\mathrm{y}=\frac{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\mp\sqrt{\mathrm{2}}−\mathrm{1}\:}{\sqrt{\mathrm{2}}−\mathrm{1}\:}\:\:\vee\:\:\:\mathrm{y}=\frac{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}+\sqrt{\mathrm{2}}\:\:+\mathrm{1}}{−\left(\sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)} \\ $$$$ \\ $$$$\mathrm{Continue} \\ $$
Commented by tawa tawa last updated on 10/Jun/17

$$\mathrm{Am}\:\mathrm{with}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 09/Jun/17
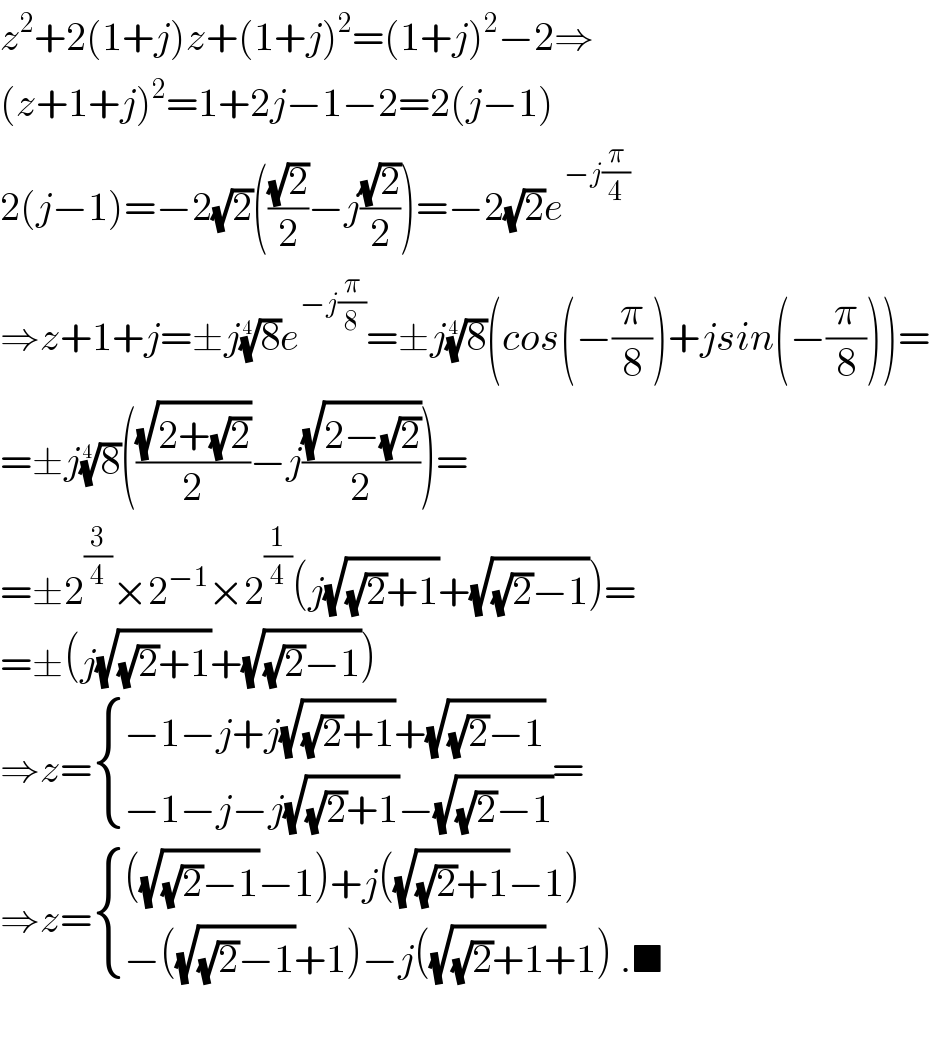
$${z}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+{j}\right){z}+\left(\mathrm{1}+{j}\right)^{\mathrm{2}} =\left(\mathrm{1}+{j}\right)^{\mathrm{2}} −\mathrm{2}\Rightarrow \\ $$$$\left({z}+\mathrm{1}+{j}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{j}−\mathrm{1}−\mathrm{2}=\mathrm{2}\left({j}−\mathrm{1}\right) \\ $$$$\mathrm{2}\left({j}−\mathrm{1}\right)=−\mathrm{2}\sqrt{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−{j}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=−\mathrm{2}\sqrt{\mathrm{2}}{e}^{−{j}\frac{\pi}{\mathrm{4}}} \\ $$$$\Rightarrow{z}+\mathrm{1}+{j}=\pm{j}\sqrt[{\mathrm{4}}]{\mathrm{8}}{e}^{−{j}\frac{\pi}{\mathrm{8}}} =\pm{j}\sqrt[{\mathrm{4}}]{\mathrm{8}}\left({cos}\left(−\frac{\pi}{\mathrm{8}}\right)+{jsin}\left(−\frac{\pi}{\mathrm{8}}\right)\right)= \\ $$$$=\pm{j}\sqrt[{\mathrm{4}}]{\mathrm{8}}\left(\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}−{j}\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{2}}\right)= \\ $$$$=\pm\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} ×\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \left({j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)= \\ $$$$=\pm\left({j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$\Rightarrow{z}=\begin{cases}{−\mathrm{1}−{j}+{j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}\\{−\mathrm{1}−{j}−{j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}\end{cases}= \\ $$$$\Rightarrow{z}=\begin{cases}{\left(\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}−\mathrm{1}\right)+{j}\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\mathrm{1}\right)}\\{−\left(\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}+\mathrm{1}\right)−{j}\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\mathrm{1}\right)\:.\blacksquare}\end{cases} \\ $$$$ \\ $$
Commented by tawa tawa last updated on 10/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 10/Jun/17

$$\mathrm{Please}\:\mathrm{sir}\:,\:\mathrm{am}\:\mathrm{still}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{workings}\:\mathrm{sir}.\: \\ $$$$\mathrm{please}\:\mathrm{sir}\:\mathrm{explain}\:\mathrm{to}\:\mathrm{me}\:\mathrm{the}\:\mathrm{steps}.\:\mathrm{i}\:\mathrm{mean}\:\mathrm{the}\:\mathrm{begining} \\ $$
Commented by tawa tawa last updated on 11/Jun/17
![Sir i am lost from. ± j(2^(3/4) )(cos(−(π/8)) + jsin(−(π/8))] why (−(π/8)) ???. How is it minus sir. i thought it is.... cos((π/8)) − jsin((π/4)) And how is it j(2^(3/4) )(((√(2 + (√2)))/2) − j((√(2 − (√(2 ))))/2)) And the next steps......](Q15487.png)
$$\mathrm{Sir}\:\mathrm{i}\:\mathrm{am}\:\mathrm{lost}\:\mathrm{from}.\:\pm\:\mathrm{j}\left(\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} \right)\left(\mathrm{cos}\left(−\frac{\pi}{\mathrm{8}}\right)\:+\:\mathrm{jsin}\left(−\frac{\pi}{\mathrm{8}}\right)\right]\: \\ $$$$\mathrm{why}\:\left(−\frac{\pi}{\mathrm{8}}\right)\:???.\:\mathrm{How}\:\mathrm{is}\:\mathrm{it}\:\mathrm{minus}\:\mathrm{sir}.\: \\ $$$$\mathrm{i}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{is}....\:\mathrm{cos}\left(\frac{\pi}{\mathrm{8}}\right)\:−\:\mathrm{jsin}\left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{And}\:\mathrm{how}\:\mathrm{is}\:\mathrm{it}\:\:\:\mathrm{j}\left(\mathrm{2}^{\mathrm{3}/\mathrm{4}} \right)\left(\frac{\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}}}}{\mathrm{2}}\:−\:\mathrm{j}\frac{\sqrt{\mathrm{2}\:−\:\sqrt{\mathrm{2}\:}}}{\mathrm{2}}\right) \\ $$$$\mathrm{And}\:\mathrm{the}\:\mathrm{next}\:\mathrm{steps}...... \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17

$$\left.\mathrm{1}\right)\left({cosx}+{jsinx}\right)^{{n}} ={cosnx}+{jsinnx} \\ $$$$\left.\mathrm{2}\right){e}^{{jx}} ={cosx}+{jsinx} \\ $$$$\left.\mathrm{3}\right){e}^{−{jx}} ={cos}\left(−{x}\right)+{jsin}\left(−{x}\right)={cosx}−{jsinx} \\ $$$${because}:\:{cos}\left(−{x}\right)={cosx},{sin}\left(−{x}\right)=−{sinx} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−{j}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}={cos}\left(−\frac{\pi}{\mathrm{4}}\right)+{jsin}\left(−\frac{\pi}{\mathrm{4}}\right)={e}^{−{j}\frac{\pi}{\mathrm{4}}} \\ $$$${angles}\:{in}\:{cos}\:\&\:{sin},{should}\:{be}\:{the}\:{same}. \\ $$$$\left({z}+\mathrm{1}+{j}\right)^{\mathrm{2}} =−\mathrm{2}\sqrt{\mathrm{2}}{e}^{−{j}\frac{\pi}{\mathrm{4}}} =\left({j}\right)^{\mathrm{2}} ×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} ×{e}^{−{j}\frac{\pi}{\mathrm{4}}} \\ $$$$\sqrt{\left({z}+\mathrm{1}+{j}\right)^{\mathrm{2}} }=\pm\sqrt{\left({j}\right)^{\mathrm{2}} ×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} ×{e}^{−{j}\frac{\pi}{\mathrm{4}}} } \\ $$$${z}+\mathrm{1}+{j}=\pm{j}×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} ×{e}^{−{j}\frac{\pi}{\mathrm{8}}} \\ $$$${e}^{−{j}\frac{\pi}{\mathrm{8}}} ={cos}\left(−\frac{\pi}{\mathrm{8}}\right)+{jsin}\left(−\frac{\pi}{\mathrm{8}}\right)={cos}\left(\frac{\pi}{\mathrm{8}}\right)−{jsin}\left(\frac{\pi}{\mathrm{8}}\right) \\ $$$${cos}\frac{\pi}{\mathrm{8}}=\sqrt{\frac{\mathrm{1}+{cos}\frac{\pi}{\mathrm{4}}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}}}=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}= \\ $$$$=\frac{\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}}{\mathrm{2}}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} ×\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$${sin}\frac{\pi}{\mathrm{8}}=\sqrt{\frac{\mathrm{1}−{cos}\frac{\pi}{\mathrm{4}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{2}}= \\ $$$$=\frac{\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} ×\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\Rightarrow{z}+\mathrm{1}+{j}=\pm{j}×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} ×\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} \left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−{j}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)= \\ $$$$=\pm\boldsymbol{{j}}×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\boldsymbol{{j}}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)= \\ $$$$=\pm\boldsymbol{{j}}×\mathrm{1}×\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\boldsymbol{{j}}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)=\pm\boldsymbol{{j}}\left(.....\right)\: \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{it}}\:\boldsymbol{{ok}}?\:\boldsymbol{{miss}}\:\boldsymbol{{tawa}}? \\ $$
Commented by tawa tawa last updated on 11/Jun/17
$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{understand}\:\mathrm{very}\:\mathrm{well}\:\mathrm{now}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate} \\ $$$$\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
