
Question Number 153404 by liberty last updated on 07/Sep/21
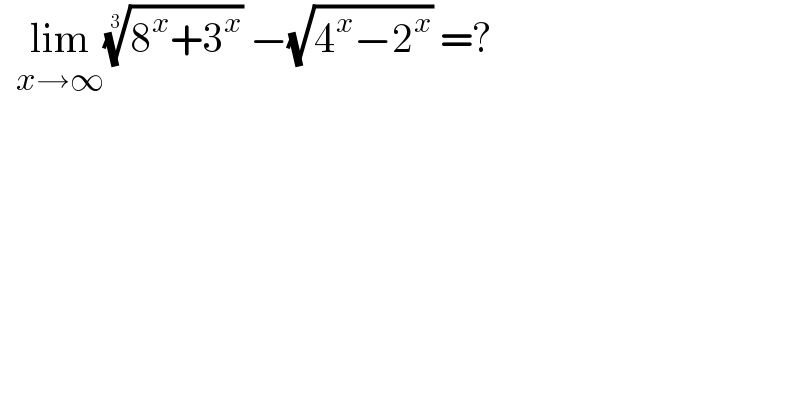
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{3}}]{\mathrm{8}^{{x}} +\mathrm{3}^{{x}} }\:−\sqrt{\mathrm{4}^{{x}} −\mathrm{2}^{{x}} }\:=? \\ $$
Answered by EDWIN88 last updated on 07/Sep/21
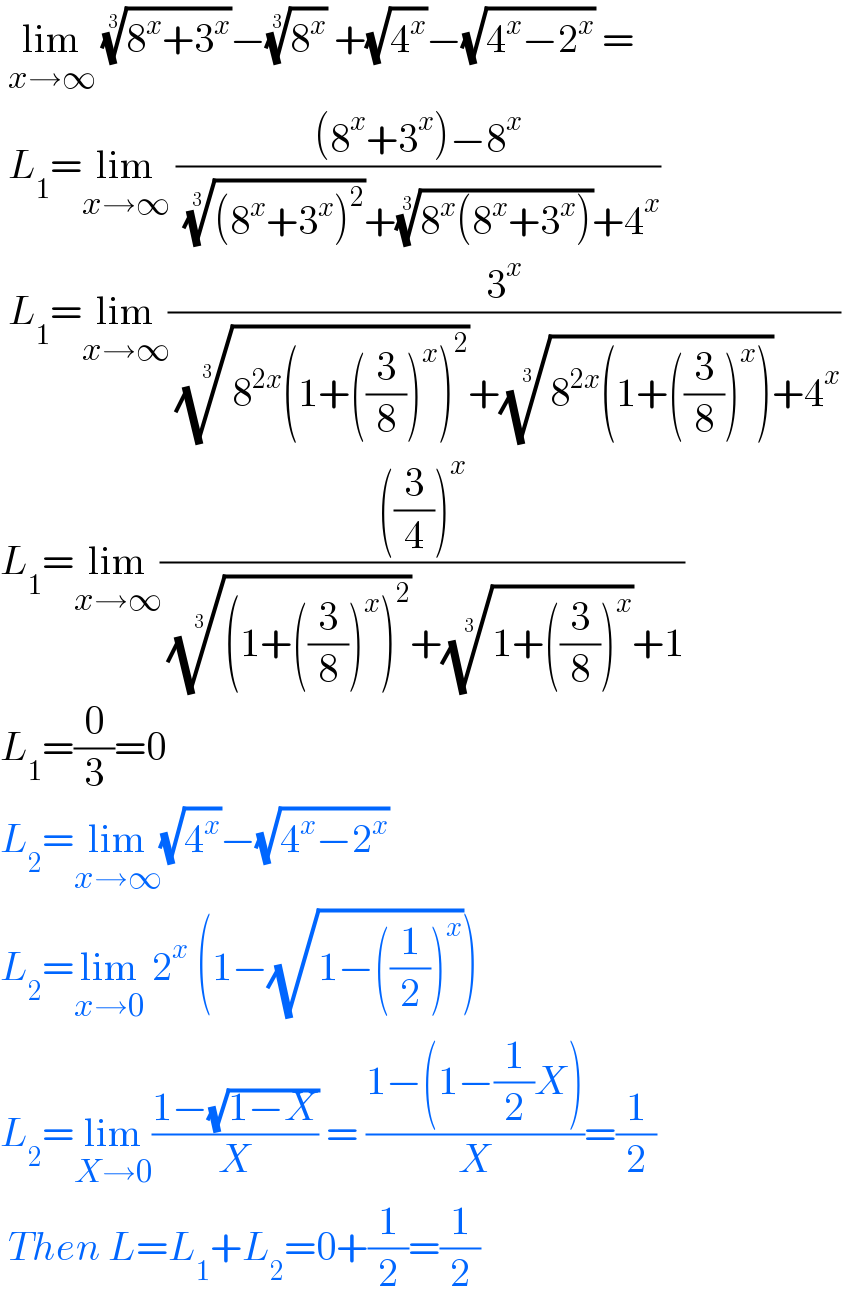
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}}]{\mathrm{8}^{{x}} +\mathrm{3}^{{x}} }−\sqrt[{\mathrm{3}}]{\mathrm{8}^{{x}} }\:+\sqrt{\mathrm{4}^{{x}} }−\sqrt{\mathrm{4}^{{x}} −\mathrm{2}^{{x}} }\:= \\ $$$$\:{L}_{\mathrm{1}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{8}^{{x}} +\mathrm{3}^{{x}} \right)−\mathrm{8}^{{x}} }{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{8}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\mathrm{8}^{{x}} \left(\mathrm{8}^{{x}} +\mathrm{3}^{{x}} \right)}+\mathrm{4}^{{x}} } \\ $$$$\:{L}_{\mathrm{1}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}^{{x}} }{\:\sqrt[{\mathrm{3}}]{\mathrm{8}^{\mathrm{2}{x}} \left(\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{x}} \right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\mathrm{8}^{\mathrm{2}{x}} \left(\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{x}} \right)}+\mathrm{4}^{{x}} } \\ $$$${L}_{\mathrm{1}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{x}} }{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{x}} \right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{x}} }+\mathrm{1}} \\ $$$${L}_{\mathrm{1}} =\frac{\mathrm{0}}{\mathrm{3}}=\mathrm{0} \\ $$$${L}_{\mathrm{2}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{4}^{{x}} }−\sqrt{\mathrm{4}^{{x}} −\mathrm{2}^{{x}} }\: \\ $$$${L}_{\mathrm{2}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{2}^{{x}} \:\left(\mathrm{1}−\sqrt{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} }\right) \\ $$$${L}_{\mathrm{2}} =\underset{{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\sqrt{\mathrm{1}−{X}}}{{X}}\:=\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{X}\right)}{{X}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:{Then}\:{L}={L}_{\mathrm{1}} +{L}_{\mathrm{2}} =\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
