
Question Number 153384 by SANOGO last updated on 06/Sep/21

Answered by mindispower last updated on 06/Sep/21
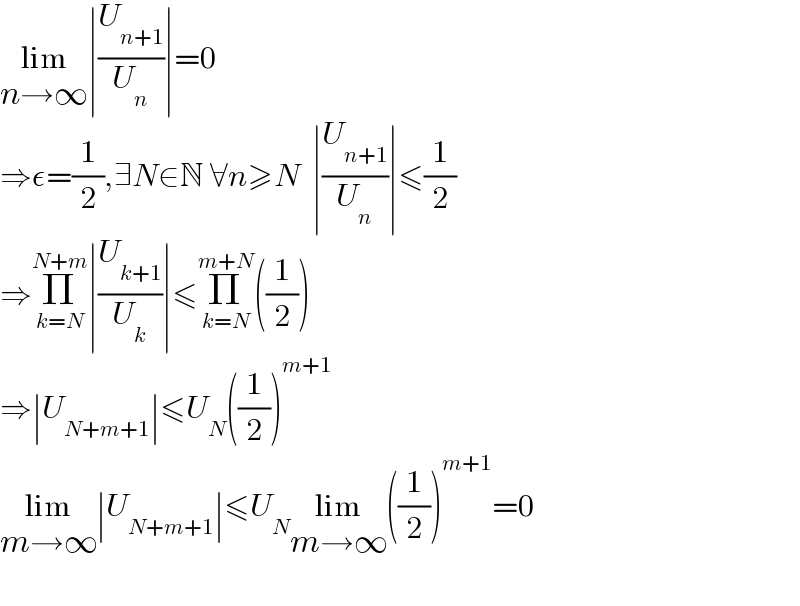
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid\frac{{U}_{{n}+\mathrm{1}} }{{U}_{{n}} }\mid=\mathrm{0} \\ $$$$\Rightarrow\epsilon=\frac{\mathrm{1}}{\mathrm{2}},\exists{N}\in\mathbb{N}\:\forall{n}\geqslant{N}\:\:\mid\frac{{U}_{{n}+\mathrm{1}} }{{U}_{{n}} }\mid\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\underset{{k}={N}} {\overset{{N}+{m}} {\prod}}\mid\frac{{U}_{{k}+\mathrm{1}} }{{U}_{{k}} }\mid\leqslant\underset{{k}={N}} {\overset{{m}+{N}} {\prod}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mid{U}_{{N}+{m}+\mathrm{1}} \mid\leqslant{U}_{{N}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{m}+\mathrm{1}} \\ $$$$\underset{{m}\rightarrow\infty} {\mathrm{lim}}\mid{U}_{{N}+{m}+\mathrm{1}} \mid\leqslant{U}_{{N}} \underset{{m}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{m}+\mathrm{1}} =\mathrm{0} \\ $$$$ \\ $$
Commented by SANOGO last updated on 07/Sep/21
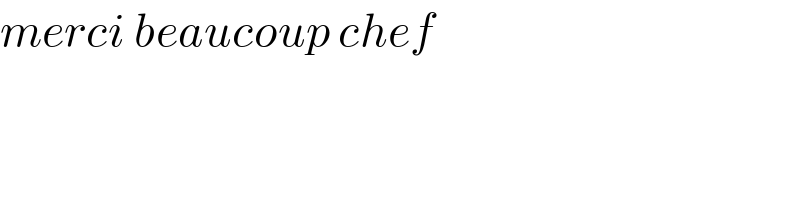
$${merci}\:{beaucoup}\:{chef} \\ $$
Answered by Jonathanwaweh last updated on 07/Sep/21
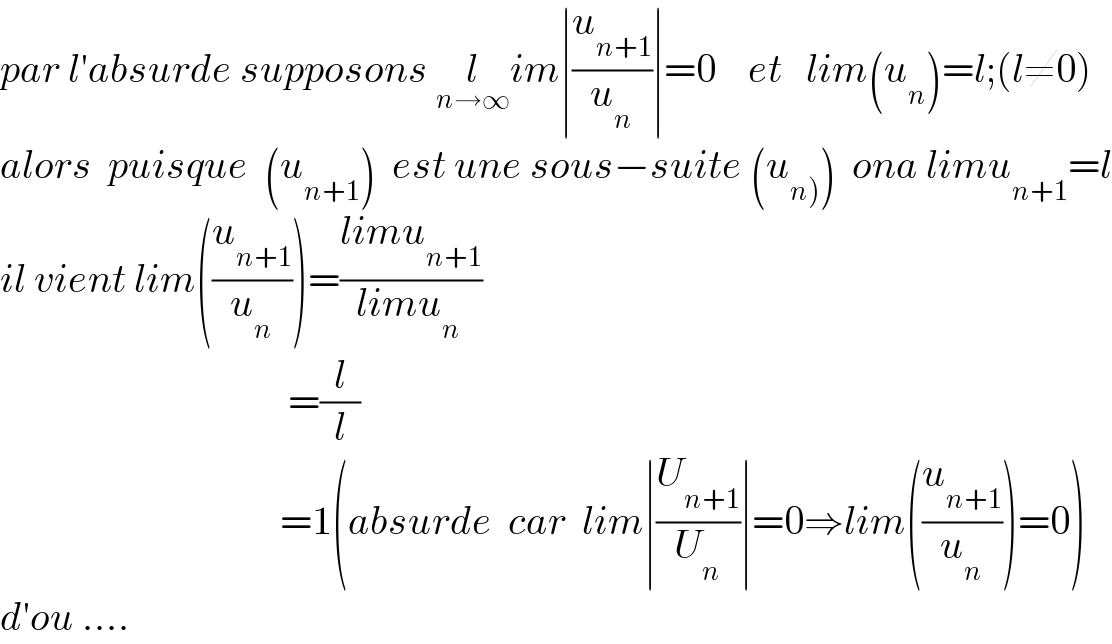
$${par}\:{l}'{absurde}\:{supposons}\:\underset{{n}\rightarrow\infty} {{l}im}\mid\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }\mid=\mathrm{0}\:\:\:\:{et}\:\:\:{lim}\left({u}_{{n}} \right)={l};\left({l}\neq\mathrm{0}\right) \\ $$$${alors}\:\:{puisque}\:\:\left({u}_{{n}+\mathrm{1}} \right)\:\:{est}\:{une}\:{sous}−{suite}\:\left({u}_{\left.{n}\right)} \right)\:\:{ona}\:{limu}_{{n}+\mathrm{1}} ={l} \\ $$$${il}\:{vient}\:{lim}\left(\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }\right)=\frac{{limu}_{{n}+\mathrm{1}} }{{limu}_{{n}\:} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{l}}{{l}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}\left({absurde}\:\:{car}\:\:{lim}\mid\frac{{U}_{{n}+\mathrm{1}} }{{U}_{{n}} }\mid=\mathrm{0}\Rightarrow{lim}\left(\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }\right)=\mathrm{0}\right) \\ $$$${d}'{ou}\:.... \\ $$
Commented by SANOGO last updated on 07/Sep/21
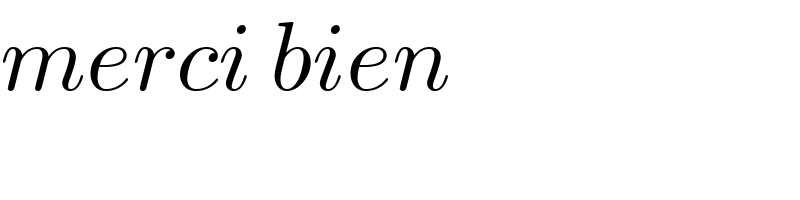
$${merci}\:{bien} \\ $$
Commented by mindispower last updated on 23/Sep/21

$${je}\:{vous}\:\:{en}\:{Prie} \\ $$
