
Question Number 15328 by tawa tawa last updated on 09/Jun/17
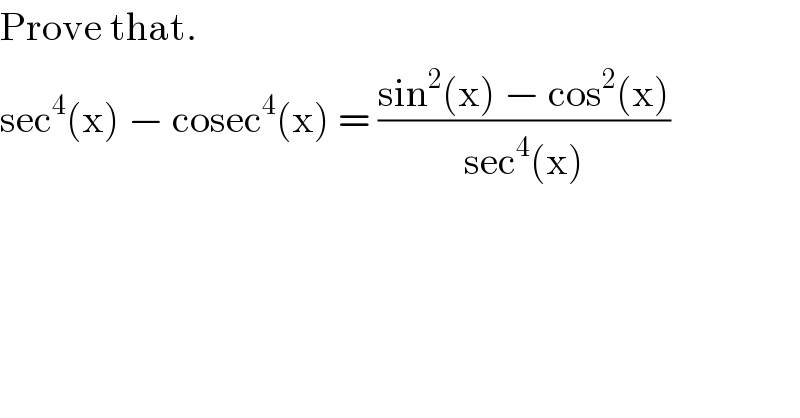
$$\mathrm{Prove}\:\mathrm{that}. \\ $$$$\mathrm{sec}^{\mathrm{4}} \left(\mathrm{x}\right)\:−\:\mathrm{cosec}^{\mathrm{4}} \left(\mathrm{x}\right)\:=\:\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\:−\:\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{sec}^{\mathrm{4}} \left(\mathrm{x}\right)} \\ $$
Answered by RasheedSoomro last updated on 10/Jun/17
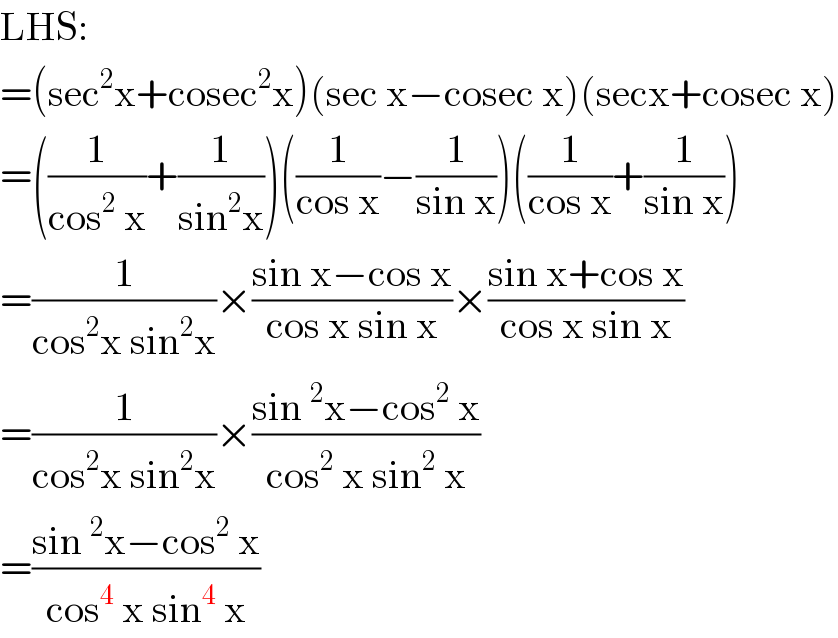
$$\mathrm{LHS}: \\ $$$$=\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}+\mathrm{cosec}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{sec}\:\mathrm{x}−\mathrm{cosec}\:\mathrm{x}\right)\left(\mathrm{secx}+\mathrm{cosec}\:\mathrm{x}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\right)\left(\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}}\right)\left(\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}}×\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}×\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}}×\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{x}} \\ $$$$=\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}}{\mathrm{cos}^{\mathrm{4}} \:\mathrm{x}\:\mathrm{sin}^{\mathrm{4}} \:\mathrm{x}} \\ $$
Commented by tawa tawa last updated on 09/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 09/Jun/17
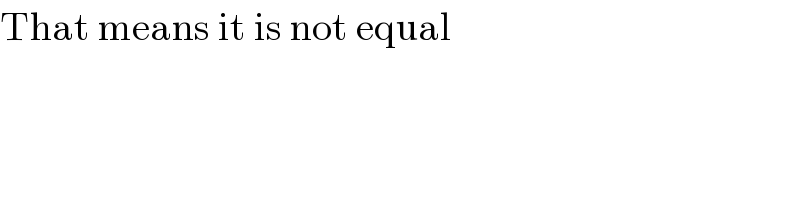
$$\mathrm{That}\:\mathrm{means}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{equal} \\ $$
Commented by RasheedSoomro last updated on 09/Jun/17

$$\mathrm{I}\:\mathrm{think}\:\mathrm{so}. \\ $$
Commented by RasheedSoomro last updated on 10/Jun/17
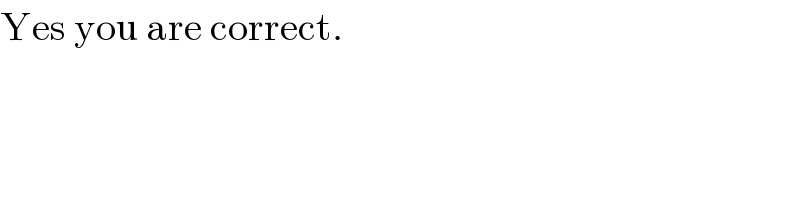
$$\mathrm{Yes}\:\mathrm{you}\:\mathrm{are}\:\mathrm{correct}. \\ $$
