
Question Number 153168 by liberty last updated on 05/Sep/21
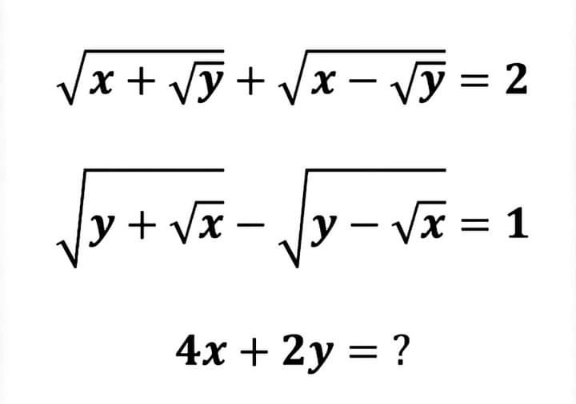
Answered by EDWIN88 last updated on 05/Sep/21
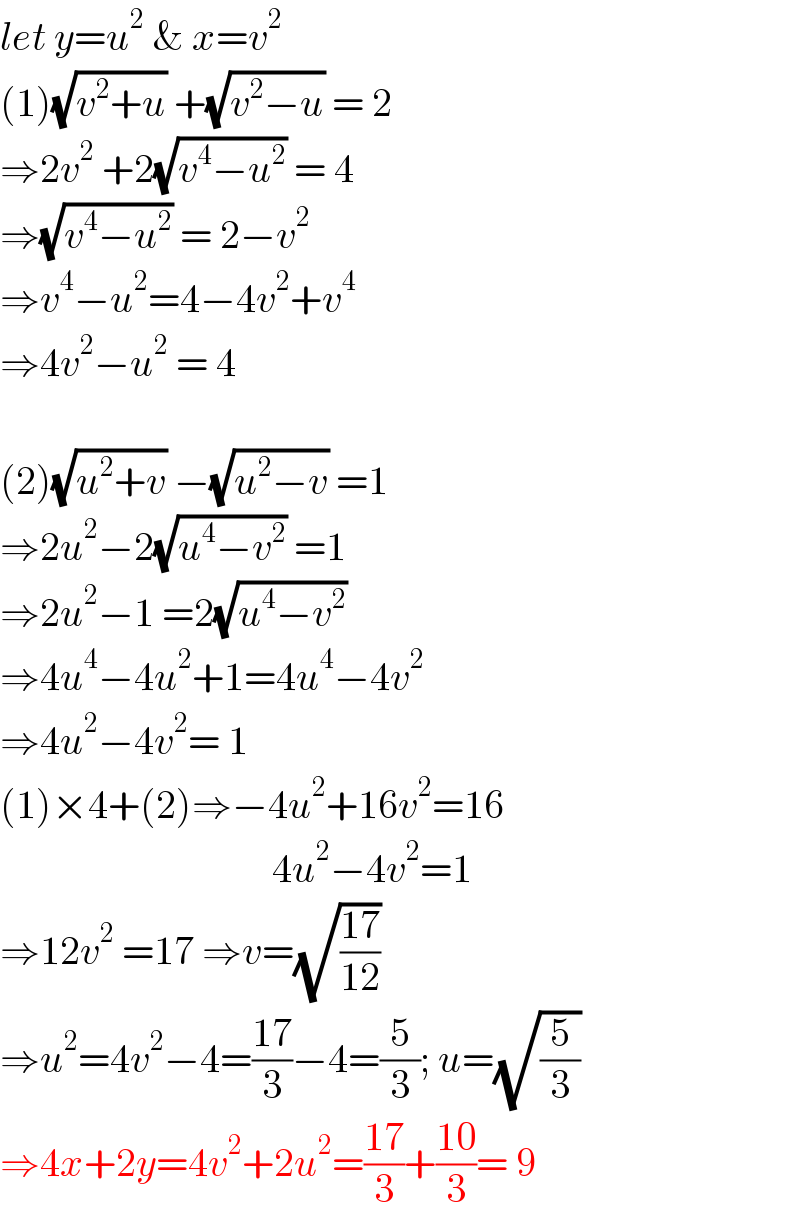
$${let}\:{y}={u}^{\mathrm{2}} \:\&\:{x}={v}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\sqrt{{v}^{\mathrm{2}} +{u}}\:+\sqrt{{v}^{\mathrm{2}} −{u}}\:=\:\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}{v}^{\mathrm{2}} \:+\mathrm{2}\sqrt{{v}^{\mathrm{4}} −{u}^{\mathrm{2}} }\:=\:\mathrm{4} \\ $$$$\Rightarrow\sqrt{{v}^{\mathrm{4}} −{u}^{\mathrm{2}} }\:=\:\mathrm{2}−{v}^{\mathrm{2}} \\ $$$$\Rightarrow{v}^{\mathrm{4}} −{u}^{\mathrm{2}} =\mathrm{4}−\mathrm{4}{v}^{\mathrm{2}} +{v}^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{4}{v}^{\mathrm{2}} −{u}^{\mathrm{2}} \:=\:\mathrm{4} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\sqrt{{u}^{\mathrm{2}} +{v}}\:−\sqrt{{u}^{\mathrm{2}} −{v}}\:=\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{u}^{\mathrm{2}} −\mathrm{2}\sqrt{{u}^{\mathrm{4}} −{v}^{\mathrm{2}} }\:=\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\:=\mathrm{2}\sqrt{{u}^{\mathrm{4}} −{v}^{\mathrm{2}} }\: \\ $$$$\Rightarrow\mathrm{4}{u}^{\mathrm{4}} −\mathrm{4}{u}^{\mathrm{2}} +\mathrm{1}=\mathrm{4}{u}^{\mathrm{4}} −\mathrm{4}{v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}{v}^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\left(\mathrm{1}\right)×\mathrm{4}+\left(\mathrm{2}\right)\Rightarrow−\mathrm{4}{u}^{\mathrm{2}} +\mathrm{16}{v}^{\mathrm{2}} =\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}{v}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{12}{v}^{\mathrm{2}} \:=\mathrm{17}\:\Rightarrow{v}=\sqrt{\frac{\mathrm{17}}{\mathrm{12}}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} =\mathrm{4}{v}^{\mathrm{2}} −\mathrm{4}=\frac{\mathrm{17}}{\mathrm{3}}−\mathrm{4}=\frac{\mathrm{5}}{\mathrm{3}};\:{u}=\sqrt{\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{4}{x}+\mathrm{2}{y}=\mathrm{4}{v}^{\mathrm{2}} +\mathrm{2}{u}^{\mathrm{2}} =\frac{\mathrm{17}}{\mathrm{3}}+\frac{\mathrm{10}}{\mathrm{3}}=\:\mathrm{9} \\ $$
