
Question Number 153130 by mathdanisur last updated on 04/Sep/21
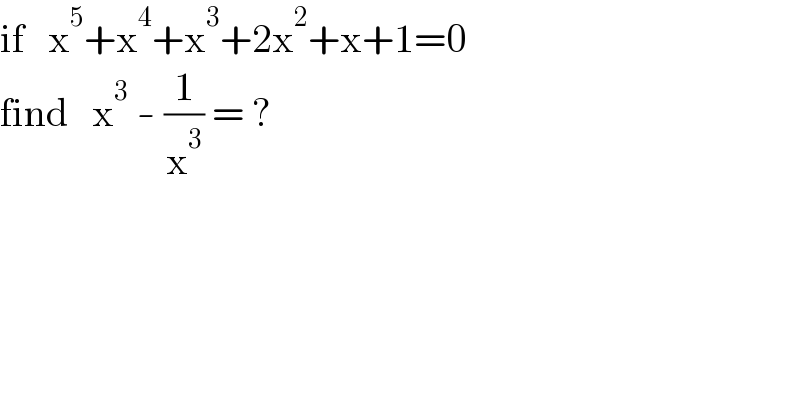
$$\mathrm{if}\:\:\:\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{3}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{find}\:\:\:\mathrm{x}^{\mathrm{3}} \:-\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:=\:? \\ $$
Answered by ajfour last updated on 05/Sep/21
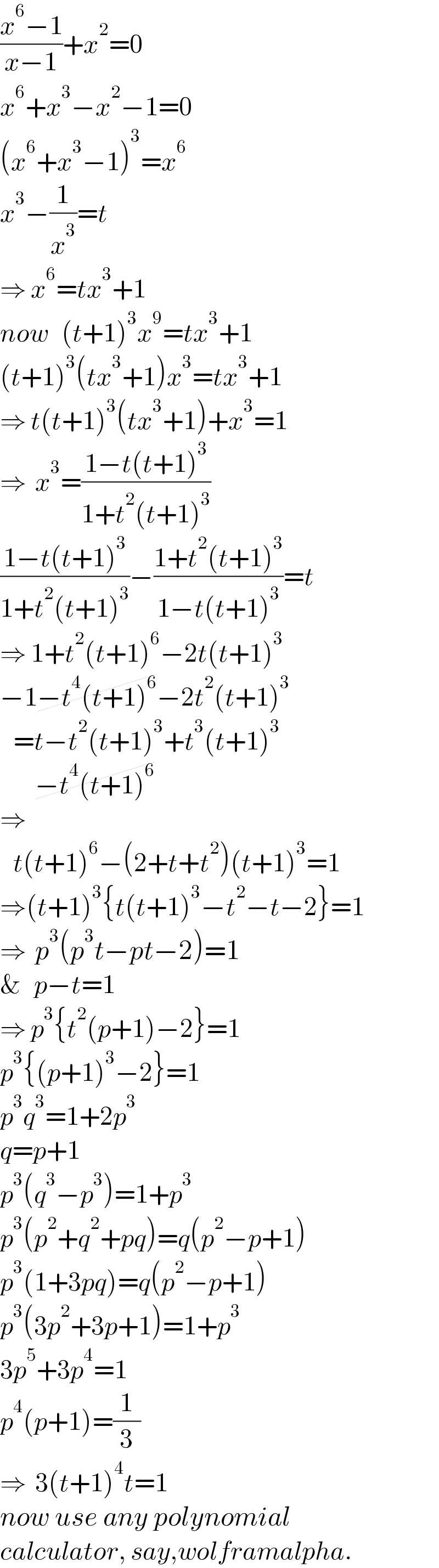
$$\frac{{x}^{\mathrm{6}} −\mathrm{1}}{{x}−\mathrm{1}}+{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{6}} +{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{6}} +{x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{3}} ={x}^{\mathrm{6}} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }={t} \\ $$$$\Rightarrow\:{x}^{\mathrm{6}} ={tx}^{\mathrm{3}} +\mathrm{1} \\ $$$${now}\:\:\:\left({t}+\mathrm{1}\right)^{\mathrm{3}} {x}^{\mathrm{9}} ={tx}^{\mathrm{3}} +\mathrm{1} \\ $$$$\left({t}+\mathrm{1}\right)^{\mathrm{3}} \left({tx}^{\mathrm{3}} +\mathrm{1}\right){x}^{\mathrm{3}} ={tx}^{\mathrm{3}} +\mathrm{1} \\ $$$$\Rightarrow\:{t}\left({t}+\mathrm{1}\right)^{\mathrm{3}} \left({tx}^{\mathrm{3}} +\mathrm{1}\right)+{x}^{\mathrm{3}} =\mathrm{1} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{3}} =\frac{\mathrm{1}−{t}\left({t}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{1}+{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\frac{\mathrm{1}−{t}\left({t}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{1}+{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{1}+{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{1}−{t}\left({t}+\mathrm{1}\right)^{\mathrm{3}} }={t} \\ $$$$\Rightarrow\:\mathrm{1}+{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{6}} −\mathrm{2}{t}\left({t}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$−\mathrm{1}\cancel{−{t}^{\mathrm{4}} \left({t}+\mathrm{1}\right)^{\mathrm{6}} }−\mathrm{2}{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:\:\:={t}−{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} +{t}^{\mathrm{3}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\cancel{−{t}^{\mathrm{4}} \left({t}+\mathrm{1}\right)^{\mathrm{6}} } \\ $$$$\Rightarrow \\ $$$$\:\:\:{t}\left({t}+\mathrm{1}\right)^{\mathrm{6}} −\left(\mathrm{2}+{t}+{t}^{\mathrm{2}} \right)\left({t}+\mathrm{1}\right)^{\mathrm{3}} =\mathrm{1} \\ $$$$\Rightarrow\left({t}+\mathrm{1}\right)^{\mathrm{3}} \left\{{t}\left({t}+\mathrm{1}\right)^{\mathrm{3}} −{t}^{\mathrm{2}} −{t}−\mathrm{2}\right\}=\mathrm{1} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{3}} \left({p}^{\mathrm{3}} {t}−{pt}−\mathrm{2}\right)=\mathrm{1} \\ $$$$\&\:\:\:{p}−{t}=\mathrm{1} \\ $$$$\Rightarrow\:{p}^{\mathrm{3}} \left\{{t}^{\mathrm{2}} \left({p}+\mathrm{1}\right)−\mathrm{2}\right\}=\mathrm{1} \\ $$$${p}^{\mathrm{3}} \left\{\left({p}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{2}\right\}=\mathrm{1} \\ $$$${p}^{\mathrm{3}} {q}^{\mathrm{3}} =\mathrm{1}+\mathrm{2}{p}^{\mathrm{3}} \\ $$$${q}={p}+\mathrm{1} \\ $$$${p}^{\mathrm{3}} \left({q}^{\mathrm{3}} −{p}^{\mathrm{3}} \right)=\mathrm{1}+{p}^{\mathrm{3}} \\ $$$${p}^{\mathrm{3}} \left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{pq}\right)={q}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right) \\ $$$${p}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{3}{pq}\right)={q}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right) \\ $$$${p}^{\mathrm{3}} \left(\mathrm{3}{p}^{\mathrm{2}} +\mathrm{3}{p}+\mathrm{1}\right)=\mathrm{1}+{p}^{\mathrm{3}} \\ $$$$\mathrm{3}{p}^{\mathrm{5}} +\mathrm{3}{p}^{\mathrm{4}} =\mathrm{1} \\ $$$${p}^{\mathrm{4}} \left({p}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{4}} {t}=\mathrm{1} \\ $$$${now}\:{use}\:{any}\:{polynomial} \\ $$$${calculator},\:{say},{wolframalpha}. \\ $$
