
Question Number 153038 by 7770 last updated on 04/Sep/21
Answered by mr W last updated on 04/Sep/21
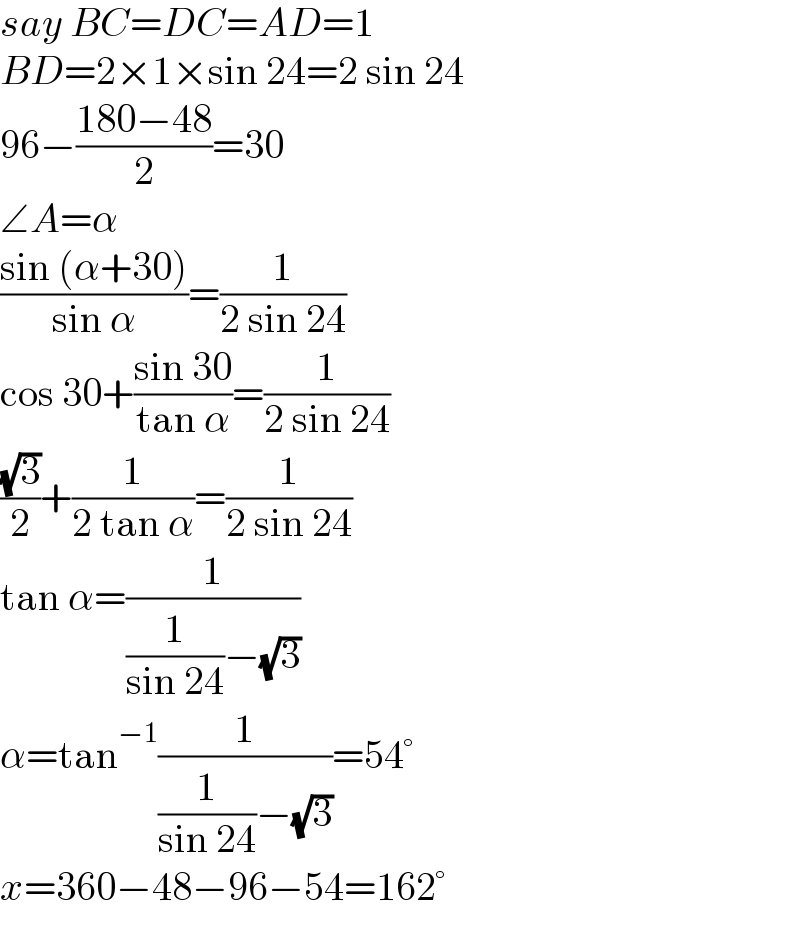
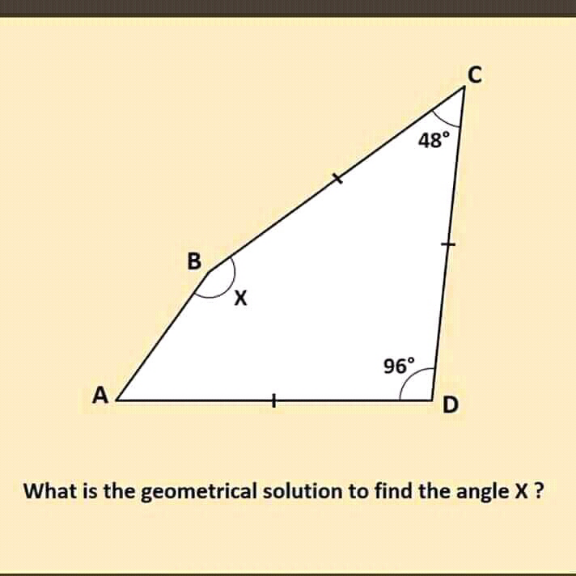
$${say}\:{BC}={DC}={AD}=\mathrm{1} \\ $$$${BD}=\mathrm{2}×\mathrm{1}×\mathrm{sin}\:\mathrm{24}=\mathrm{2}\:\mathrm{sin}\:\mathrm{24} \\ $$$$\mathrm{96}−\frac{\mathrm{180}−\mathrm{48}}{\mathrm{2}}=\mathrm{30} \\ $$$$\angle{A}=\alpha \\ $$$$\frac{\mathrm{sin}\:\left(\alpha+\mathrm{30}\right)}{\mathrm{sin}\:\alpha}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{24}} \\ $$$$\mathrm{cos}\:\mathrm{30}+\frac{\mathrm{sin}\:\mathrm{30}}{\mathrm{tan}\:\alpha}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{24}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{tan}\:\alpha}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{24}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{24}}−\sqrt{\mathrm{3}}} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{24}}−\sqrt{\mathrm{3}}}=\mathrm{54}° \\ $$$${x}=\mathrm{360}−\mathrm{48}−\mathrm{96}−\mathrm{54}=\mathrm{162}° \\ $$
Commented by Tawa11 last updated on 04/Sep/21

$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$
Commented by otchereabdullai@gmail.com last updated on 08/Sep/21

$$\mathrm{wow}! \\ $$
