Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 153006 by GalaxyBills last updated on 04/Sep/21

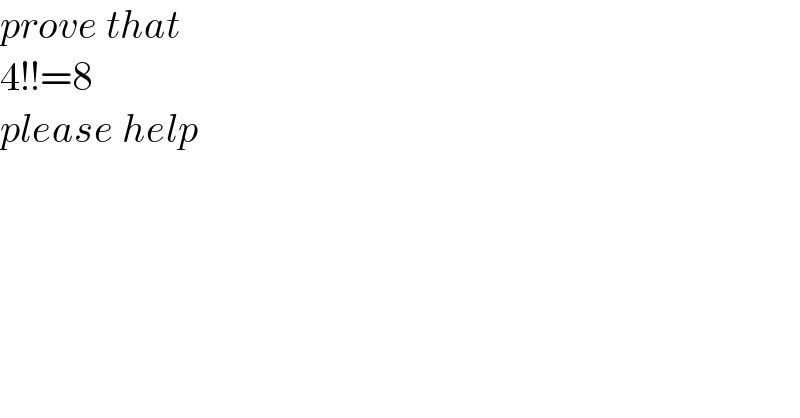
prove that 4!!=8 please help

$${prove}\:{that}\: \\ $$$$\mathrm{4}!!=\mathrm{8} \\ $$$${please}\:{help} \\ $$

Commented by talminator2856791 last updated on 04/Sep/21

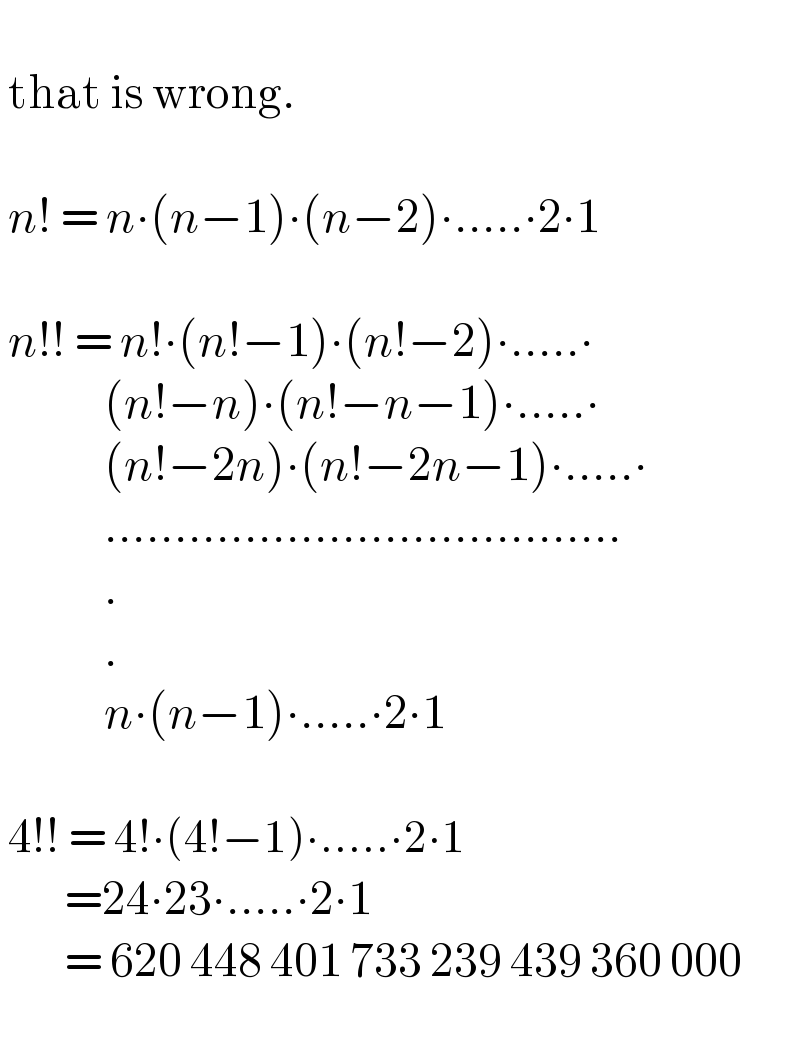
that is wrong. n! = n∙(n−1)∙(n−2)∙.....∙2∙1 n!! = n!∙(n!−1)∙(n!−2)∙.....∙ (n!−n)∙(n!−n−1)∙.....∙ (n!−2n)∙(n!−2n−1)∙.....∙ ..................................... . . n∙(n−1)∙.....∙2∙1 4!! = 4!∙(4!−1)∙.....∙2∙1 =24∙23∙.....∙2∙1 = 620 448 401 733 239 439 360 000

$$\: \\ $$$$\:\mathrm{that}\:\mathrm{is}\:\mathrm{wrong}. \\ $$$$\: \\ $$$$\:{n}!\:=\:{n}\centerdot\left({n}−\mathrm{1}\right)\centerdot\left({n}−\mathrm{2}\right)\centerdot.....\centerdot\mathrm{2}\centerdot\mathrm{1} \\ $$$$\: \\ $$$$\:{n}!!\:=\:{n}!\centerdot\left({n}!−\mathrm{1}\right)\centerdot\left({n}!−\mathrm{2}\right)\centerdot.....\centerdot \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left({n}!−{n}\right)\centerdot\left({n}!−{n}−\mathrm{1}\right)\centerdot.....\centerdot \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left({n}!−\mathrm{2}{n}\right)\centerdot\left({n}!−\mathrm{2}{n}−\mathrm{1}\right)\centerdot.....\centerdot \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:..................................... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{n}\centerdot\left({n}−\mathrm{1}\right)\centerdot.....\centerdot\mathrm{2}\centerdot\mathrm{1} \\ $$$$\:\: \\ $$$$\:\mathrm{4}!!\:=\:\mathrm{4}!\centerdot\left(\mathrm{4}!−\mathrm{1}\right)\centerdot.....\centerdot\mathrm{2}\centerdot\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{24}\centerdot\mathrm{23}\centerdot.....\centerdot\mathrm{2}\centerdot\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{620}\:\mathrm{448}\:\mathrm{401}\:\mathrm{733}\:\mathrm{239}\:\mathrm{439}\:\mathrm{360}\:\mathrm{000} \\ $$$$\: \\ $$

Commented by mr W last updated on 04/Sep/21

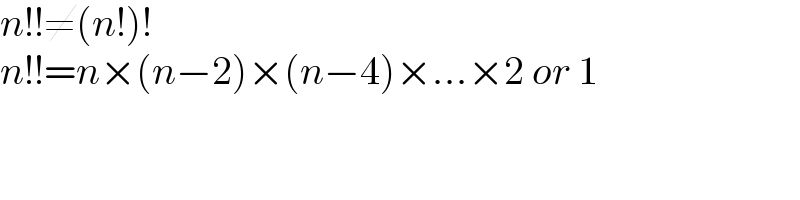
n!!≠(n!)! n!!=n×(n−2)×(n−4)×...×2 or 1

$${n}!!\neq\left({n}!\right)! \\ $$$${n}!!={n}×\left({n}−\mathrm{2}\right)×\left({n}−\mathrm{4}\right)×...×\mathrm{2}\:{or}\:\mathrm{1} \\ $$

Commented by mr W last updated on 04/Sep/21

there is no why, just know it if you didn′t already know.

$${there}\:{is}\:{no}\:{why},\:{just}\:{know}\:{it}\:{if}\:{you} \\ $$$${didn}'{t}\:{already}\:{know}. \\ $$

Commented by talminator2856791 last updated on 04/Sep/21

why?

$$\:\mathrm{why}? \\ $$

Commented by talminator2856791 last updated on 04/Sep/21

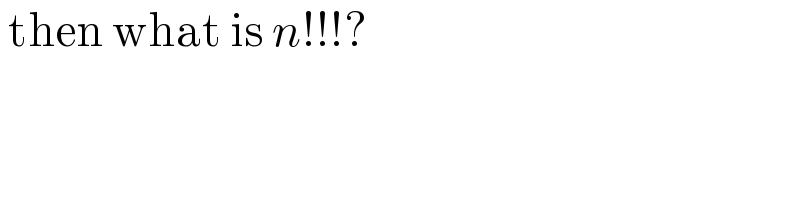
then what is n!!!?

$$\:\mathrm{then}\:\mathrm{what}\:\mathrm{is}\:{n}!!!? \\ $$

Commented by mr W last updated on 04/Sep/21

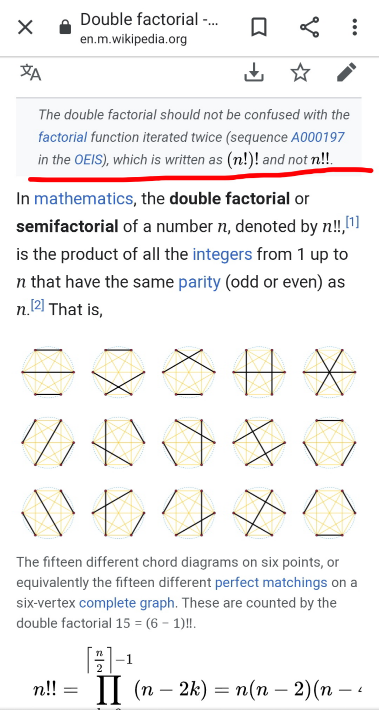
Commented by mr W last updated on 04/Sep/21

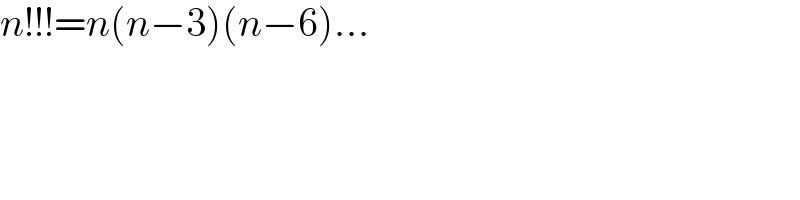
n!!!=n(n−3)(n−6)...

$${n}!!!={n}\left({n}−\mathrm{3}\right)\left({n}−\mathrm{6}\right)... \\ $$

Commented by Rasheed.Sindhi last updated on 04/Sep/21

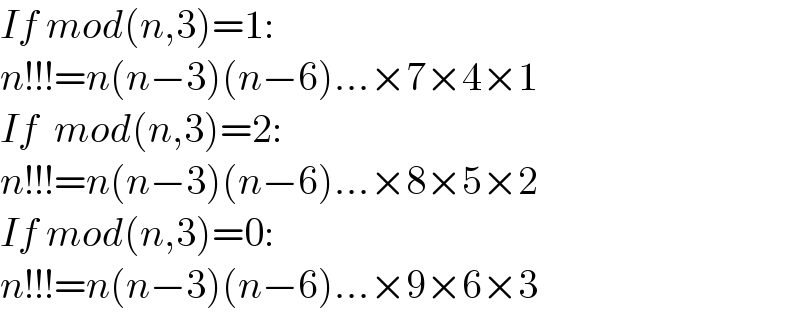
If mod(n,3)=1: n!!!=n(n−3)(n−6)...×7×4×1 If mod(n,3)=2: n!!!=n(n−3)(n−6)...×8×5×2 If mod(n,3)=0: n!!!=n(n−3)(n−6)...×9×6×3

$${If}\:{mod}\left({n},\mathrm{3}\right)=\mathrm{1}: \\ $$$${n}!!!={n}\left({n}−\mathrm{3}\right)\left({n}−\mathrm{6}\right)...×\mathrm{7}×\mathrm{4}×\mathrm{1} \\ $$$${If}\:\:{mod}\left({n},\mathrm{3}\right)=\mathrm{2}: \\ $$$${n}!!!={n}\left({n}−\mathrm{3}\right)\left({n}−\mathrm{6}\right)...×\mathrm{8}×\mathrm{5}×\mathrm{2} \\ $$$${If}\:{mod}\left({n},\mathrm{3}\right)=\mathrm{0}: \\ $$$${n}!!!={n}\left({n}−\mathrm{3}\right)\left({n}−\mathrm{6}\right)...×\mathrm{9}×\mathrm{6}×\mathrm{3} \\ $$

Answered by puissant last updated on 04/Sep/21

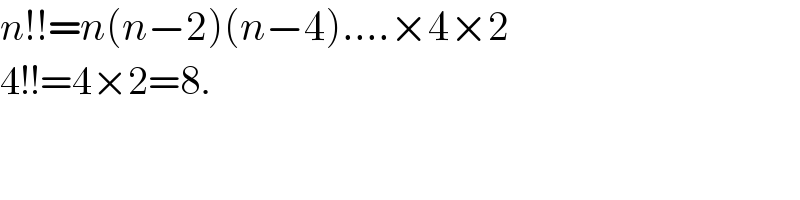
n!!=n(n−2)(n−4)....×4×2 4!!=4×2=8.

$${n}!!={n}\left({n}−\mathrm{2}\right)\left({n}−\mathrm{4}\right)....×\mathrm{4}×\mathrm{2} \\ $$$$\mathrm{4}!!=\mathrm{4}×\mathrm{2}=\mathrm{8}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com