
Question Number 15300 by Tinkutara last updated on 09/Jun/17
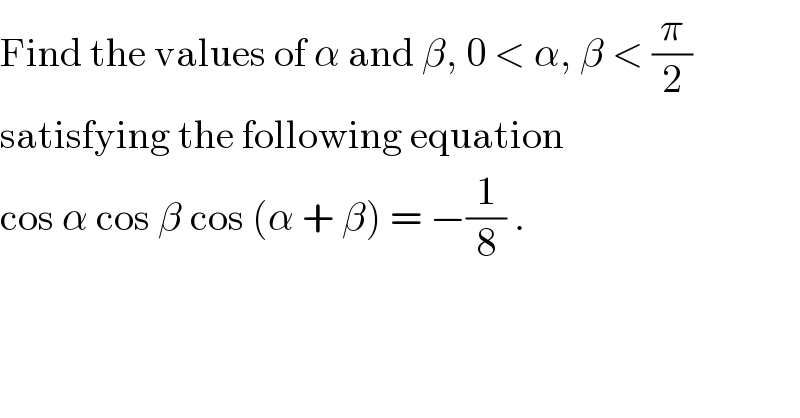
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\alpha\:\mathrm{and}\:\beta,\:\mathrm{0}\:<\:\alpha,\:\beta\:<\:\frac{\pi}{\mathrm{2}} \\ $$ $$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{following}\:\mathrm{equation} \\ $$ $$\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:=\:−\frac{\mathrm{1}}{\mathrm{8}}\:. \\ $$
Commented bymrW1 last updated on 09/Jun/17

$$\alpha=\beta=\frac{\pi}{\mathrm{3}} \\ $$
Commented bymrW1 last updated on 10/Jun/17
![F(α,β)=cos α cos β cos (α + β) let′s find the minimum of this function (∂F/∂α)=−sin α cos β cos (α+β)−cos α cos β sin (α+β) =−cos β [sin α cos (α+β)+cos α sin (α+β)] =−cos β sin (2α+β)=0 ⇒ sin (2α+β)=0 ⇒ 2α+β=π ...(i) (∂F/∂β)=−cos α sin β cos (α+β)−cos α cos β sin (α+β) =−cos α [sin β cos (α+β)+cos β sin (α+β)] =−cos α sin (α+2β)=0 ⇒ sin (α+2β)=0 ⇒ α+2β=π ...(ii) from (i) and (ii) ⇒α=β=(π/3) minimum =cos (π/3) cos (π/3) cos ((2π)/3)=−(1/8) ∴ for cos α cos β cos (α + β) = −(1/8) there is only one solution: α=β=(π/3)](Q15388.png)
$$\mathrm{F}\left(\alpha,\beta\right)=\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right) \\ $$ $$\mathrm{let}'\mathrm{s}\:\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{this}\:\mathrm{function} \\ $$ $$\frac{\partial\mathrm{F}}{\partial\alpha}=−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta\:\mathrm{cos}\:\left(\alpha+\beta\right)−\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$ $$=−\mathrm{cos}\:\beta\:\left[\mathrm{sin}\:\alpha\:\mathrm{cos}\:\left(\alpha+\beta\right)+\mathrm{cos}\:\alpha\:\:\mathrm{sin}\:\left(\alpha+\beta\right)\right] \\ $$ $$=−\mathrm{cos}\:\beta\:\mathrm{sin}\:\left(\mathrm{2}\alpha+\beta\right)=\mathrm{0} \\ $$ $$\Rightarrow\:\mathrm{sin}\:\left(\mathrm{2}\alpha+\beta\right)=\mathrm{0} \\ $$ $$\Rightarrow\:\mathrm{2}\alpha+\beta=\pi\:\:\:\:\:\:...\left(\mathrm{i}\right) \\ $$ $$\frac{\partial\mathrm{F}}{\partial\beta}=−\mathrm{cos}\:\:\alpha\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\left(\alpha+\beta\right)−\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$ $$=−\mathrm{cos}\:\alpha\:\left[\mathrm{sin}\:\beta\:\mathrm{cos}\:\left(\alpha+\beta\right)+\mathrm{cos}\:\beta\:\:\mathrm{sin}\:\left(\alpha+\beta\right)\right] \\ $$ $$=−\mathrm{cos}\:\alpha\:\mathrm{sin}\:\left(\alpha+\mathrm{2}\beta\right)=\mathrm{0} \\ $$ $$\Rightarrow\:\mathrm{sin}\:\left(\alpha+\mathrm{2}\beta\right)=\mathrm{0} \\ $$ $$\Rightarrow\:\alpha+\mathrm{2}\beta=\pi\:\:\:\:\:\:...\left(\mathrm{ii}\right) \\ $$ $$ \\ $$ $$\mathrm{from}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right) \\ $$ $$\Rightarrow\alpha=\beta=\frac{\pi}{\mathrm{3}} \\ $$ $$\mathrm{minimum}\:=\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{8}} \\ $$ $$\therefore\:\mathrm{for}\:\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:=\:−\frac{\mathrm{1}}{\mathrm{8}} \\ $$ $$\mathrm{there}\:\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution}: \\ $$ $$\alpha=\beta=\frac{\pi}{\mathrm{3}} \\ $$
Commented byTinkutara last updated on 10/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by Tinkutara last updated on 09/Jul/17
![8 cos α cos β cos (α + β) + 1 = 0 4 cos (α + β) [cos (α + β) + cos (α − β)] + 1 = 0 4 cos^2 (α + β) + 4 cos (α + β) cos (α − β) + cos^2 (α − β) + sin^2 (α − β) = 0 [2 cos (α + β) + cos (α − β)]^2 + sin^2 (α − β) = 0 sin (α − β) = 0 and 2 cos (α + β) + cos (α − β) = 0 ⇒ α = β and this gives 2 cos 2α + 1 = 0 ⇒ α = (π/3), as 0 < α, β < (π/2). So 𝛂 = 𝛃 = (𝛑/3).](Q17681.png)
$$\mathrm{8}\:\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$ $$\mathrm{4}\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:\left[\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:+\:\mathrm{cos}\:\left(\alpha\:−\:\beta\right)\right]\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$ $$\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\left(\alpha\:+\:\beta\right)\:+\:\mathrm{4}\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:\mathrm{cos}\:\left(\alpha\:−\:\beta\right) \\ $$ $$+\:\mathrm{cos}^{\mathrm{2}} \:\left(\alpha\:−\:\beta\right)\:+\:\mathrm{sin}^{\mathrm{2}} \:\left(\alpha\:−\:\beta\right)\:=\:\mathrm{0} \\ $$ $$\left[\mathrm{2}\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:+\:\mathrm{cos}\:\left(\alpha\:−\:\beta\right)\right]^{\mathrm{2}} \:+\:\mathrm{sin}^{\mathrm{2}} \:\left(\alpha\:−\:\beta\right)\:=\:\mathrm{0} \\ $$ $$\mathrm{sin}\:\left(\alpha\:−\:\beta\right)\:=\:\mathrm{0}\:\mathrm{and}\:\mathrm{2}\:\mathrm{cos}\:\left(\alpha\:+\:\beta\right)\:+\:\mathrm{cos}\:\left(\alpha\:−\:\beta\right)\:=\:\mathrm{0} \\ $$ $$\Rightarrow\:\alpha\:=\:\beta\:\mathrm{and}\:\mathrm{this}\:\mathrm{gives} \\ $$ $$\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\alpha\:+\:\mathrm{1}\:=\:\mathrm{0}\:\Rightarrow\:\alpha\:=\:\frac{\pi}{\mathrm{3}},\:\mathrm{as}\:\mathrm{0}\:<\:\alpha,\:\beta\:<\:\frac{\pi}{\mathrm{2}}. \\ $$ $$\mathrm{So}\:\boldsymbol{\alpha}\:=\:\boldsymbol{\beta}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{3}}. \\ $$
