
Question Number 152947 by mnjuly1970 last updated on 03/Sep/21
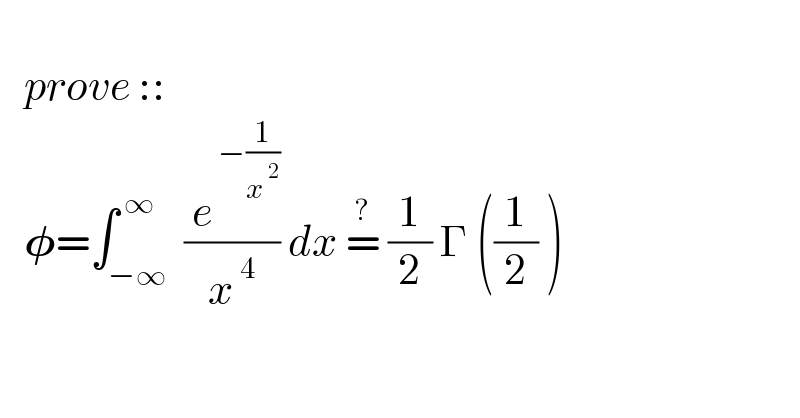
$$ \\ $$$$\:\:\:{prove}\::: \\ $$$$\:\:\:\boldsymbol{\phi}=\int_{−\infty} ^{\:\infty} \:\frac{\:{e}^{\:−\frac{\mathrm{1}}{{x}^{\:\mathrm{2}} }} }{{x}^{\:\mathrm{4}} }\:{dx}\:\overset{?} {=}\:\frac{\mathrm{1}}{\mathrm{2}}\:\Gamma\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:\right) \\ $$$$ \\ $$
Answered by mindispower last updated on 03/Sep/21
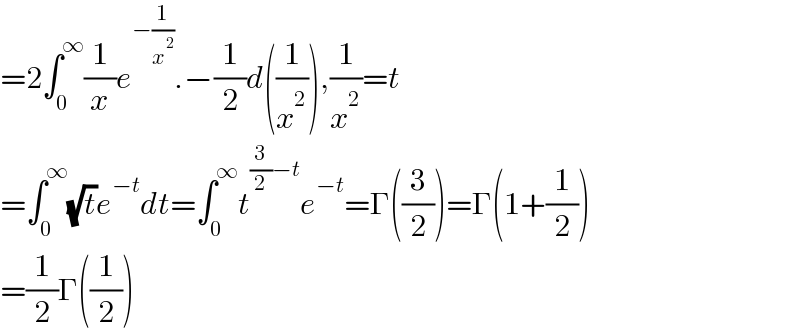
$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}}{e}^{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} .−\frac{\mathrm{1}}{\mathrm{2}}{d}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right),\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={t} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \sqrt{{t}}{e}^{−{t}} {dt}=\int_{\mathrm{0}} ^{\infty} {t}^{\frac{\mathrm{3}}{\mathrm{2}}−{t}} {e}^{−{t}} =\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
