
Question Number 152939 by mnjuly1970 last updated on 03/Sep/21
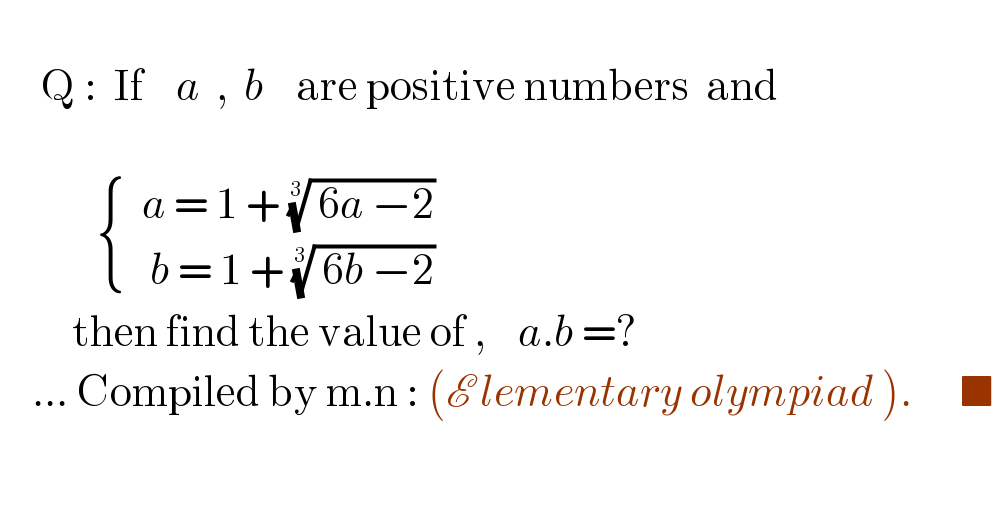
$$ \\ $$$$\:\:\:\:\:\mathrm{Q}\::\:\:\mathrm{If}\:\:\:\:{a}\:\:,\:\:{b}\:\:\:\:\mathrm{are}\:\mathrm{positive}\:\mathrm{numbers}\:\:\mathrm{and} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{\:\:{a}\:=\:\mathrm{1}\:+\:\sqrt[{\mathrm{3}}]{\:\mathrm{6}{a}\:−\mathrm{2}}\:\:}\\{\:\:\:{b}\:=\:\mathrm{1}\:+\:\sqrt[{\mathrm{3}}]{\:\mathrm{6}{b}\:−\mathrm{2}}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:,\:\:\:\:{a}.{b}\:=? \\ $$$$\:\:\:\:...\:\mathrm{Compiled}\:\mathrm{by}\:\mathrm{m}.\mathrm{n}\::\:\left(\mathscr{E}\:{lementary}\:{olympiad}\:\right).\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$
Answered by mr W last updated on 03/Sep/21
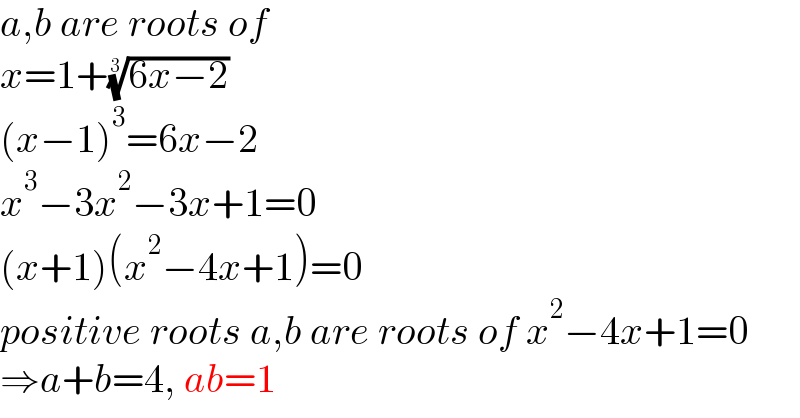
$${a},{b}\:{are}\:{roots}\:{of} \\ $$$${x}=\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{6}{x}−\mathrm{2}} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{3}} =\mathrm{6}{x}−\mathrm{2} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${positive}\:{roots}\:{a},{b}\:{are}\:{roots}\:{of}\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{a}+{b}=\mathrm{4},\:{ab}=\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 03/Sep/21

$$\:{bravo}\:{sir}\:{W}\:.{grateful}.. \\ $$
Commented by mr W last updated on 03/Sep/21
$${thanks}\:{for}\:{the}\:{nice}\:{questions}\:{sir}! \\ $$
