
Question Number 152900 by SANOGO last updated on 03/Sep/21

Answered by mindispower last updated on 03/Sep/21
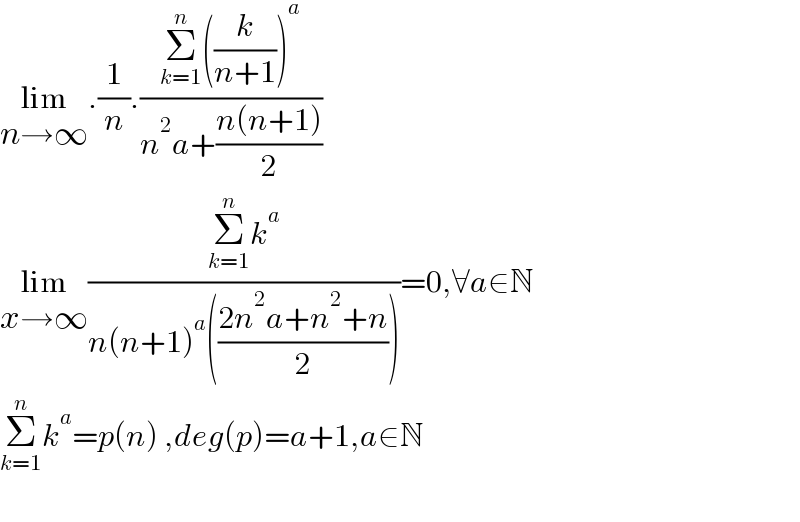
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}.\frac{\mathrm{1}}{{n}}.\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{{k}}{{n}+\mathrm{1}}\right)^{{a}} }{{n}^{\mathrm{2}} {a}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{{a}} }{{n}\left({n}+\mathrm{1}\right)^{{a}} \left(\frac{\mathrm{2}{n}^{\mathrm{2}} {a}+{n}^{\mathrm{2}} +{n}}{\mathrm{2}}\right)}=\mathrm{0},\forall{a}\in\mathbb{N} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{{a}} ={p}\left({n}\right)\:,{deg}\left({p}\right)={a}+\mathrm{1},{a}\in\mathbb{N} \\ $$$$ \\ $$
Commented by SANOGO last updated on 03/Sep/21
$${merci}\:{bien}\:{chef} \\ $$
