
Question Number 152898 by bobhans last updated on 02/Sep/21

Commented by mathdanisur last updated on 03/Sep/21
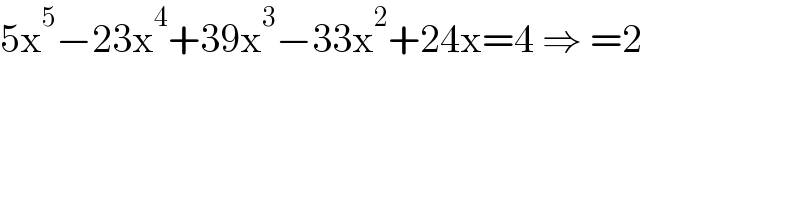
$$\mathrm{5x}^{\mathrm{5}} −\mathrm{23x}^{\mathrm{4}} +\mathrm{39x}^{\mathrm{3}} −\mathrm{33x}^{\mathrm{2}} +\mathrm{24x}=\mathrm{4}\:\Rightarrow\:=\mathrm{2} \\ $$
Commented by MJS_new last updated on 03/Sep/21

$$\mathrm{solution}\:\mathrm{please} \\ $$
Answered by mindispower last updated on 03/Sep/21

$$\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\mathrm{2}+\frac{\mathrm{1}+{x}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\right)=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}} \\ $$$$\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\right)=\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{5}{x}−{x}^{\mathrm{2}} }{\mathrm{2}{x}} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} +\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}+\mathrm{2}\left(\mathrm{1}+{x}\right)\right)=\left(\frac{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}}{\mathrm{2}{x}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{x}^{\mathrm{2}} \left(\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}\right)+\left(\mathrm{1}+{x}\right)+\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right) \\ $$$$=\left(\mathrm{1}−{x}\right)\left({x}^{\mathrm{4}} +\mathrm{25}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{4}−\mathrm{20}{x}+\mathrm{4}{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{4}{x}^{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}\right)=\left(\mathrm{1}−{x}\right)\left({x}^{\mathrm{4}} +\mathrm{29}{x}^{\mathrm{2}} −\mathrm{30}{x}+\mathrm{4}\right) \\ $$$$\mathrm{5}{x}^{\mathrm{5}} −\mathrm{13}{x}^{\mathrm{4}} +\mathrm{29}{x}^{\mathrm{3}} −\mathrm{43}{x}^{\mathrm{2}} +\mathrm{34}{x}−\mathrm{4}=\mathrm{0}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 03/Sep/21
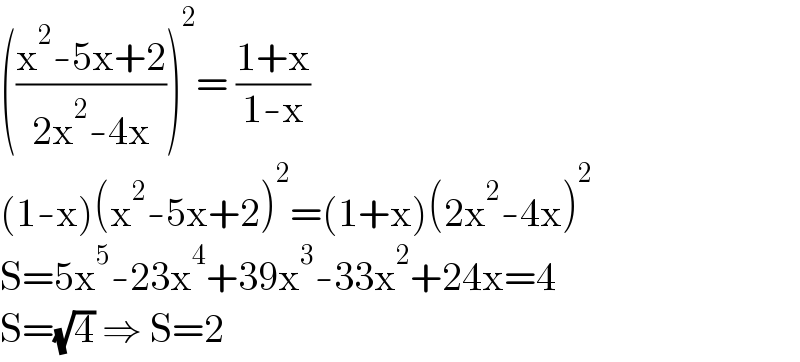
$$\left(\frac{\mathrm{x}^{\mathrm{2}} -\mathrm{5x}+\mathrm{2}}{\mathrm{2x}^{\mathrm{2}} -\mathrm{4x}}\right)^{\mathrm{2}} =\:\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}-\mathrm{x}} \\ $$$$\left(\mathrm{1}-\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} -\mathrm{5x}+\mathrm{2}\right)^{\mathrm{2}} =\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{2x}^{\mathrm{2}} -\mathrm{4x}\right)^{\mathrm{2}} \\ $$$$\mathrm{S}=\mathrm{5x}^{\mathrm{5}} -\mathrm{23x}^{\mathrm{4}} +\mathrm{39x}^{\mathrm{3}} -\mathrm{33x}^{\mathrm{2}} +\mathrm{24x}=\mathrm{4} \\ $$$$\mathrm{S}=\sqrt{\mathrm{4}}\:\Rightarrow\:\mathrm{S}=\mathrm{2} \\ $$
