
Question Number 152840 by liberty last updated on 02/Sep/21
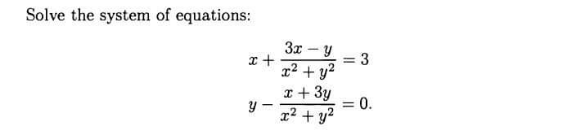
Answered by MJS_new last updated on 04/Sep/21
![transforming ⇒ x^3 −3x^2 +(y^2 +3)x−y(3y+1)=0 x^2 −(1/y)x+y^2 −3=0 y=px and transforming ⇒ x(x^2 −3x−((p−3)/(p^2 +1)))=0 [x=0 ⇒ y=0 not possible] x^2 −((3p+1)/(p(p^2 +1)))=0 ⇒ x^2 −3x−((p−3)/(p^2 +1))=0 x^2 −((3p+1)/(p(p^2 +1)))=0 substracting and solving for x ⇒ x=−((p^2 −6p−1)/(3p(p^2 +1))) inserting and transforming ⇒ p^6 −((135)/(26))p^5 −((159)/(26))p^4 +(9/(13))p^3 +((12)/(13))p^2 +(9/(26))p+(1/(26))=0 (p−(1/2))(p+1)(p^2 −6p−1)(p^2 +(4/(13))p+(1/(13)))=0 ⇒ p=−1 ⇒ x=1∧y=−1 ★ p=3−(√(10)) ⇒ x=y=0 impossible p=(1/2) ⇒ x=2∧y=1 ★ p=3+(√(10)) ⇒ x=y=0 impossible p=−(2/(13))+(3/(13))i ⇒ x=(3/2)−i∧y=(1/2)i ★ p=−(2/(13))−(3/(13i)) ⇒ x=(3/2)+i∧y=−(1/2)i ★](Q153088.png)
$$\mathrm{transforming}\:\Rightarrow \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\left({y}^{\mathrm{2}} +\mathrm{3}\right){x}−{y}\left(\mathrm{3}{y}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{1}}{{y}}{x}+{y}^{\mathrm{2}} −\mathrm{3}=\mathrm{0} \\ $$$${y}={px}\:\mathrm{and}\:\mathrm{transforming}\:\Rightarrow \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}−\frac{{p}−\mathrm{3}}{{p}^{\mathrm{2}} +\mathrm{1}}\right)=\mathrm{0}\:\left[{x}=\mathrm{0}\:\Rightarrow\:{y}=\mathrm{0}\:\mathrm{not}\:\mathrm{possible}\right] \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{3}{p}+\mathrm{1}}{{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}−\frac{{p}−\mathrm{3}}{{p}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{3}{p}+\mathrm{1}}{{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}=\mathrm{0} \\ $$$$\mathrm{substracting}\:\mathrm{and}\:\mathrm{solving}\:\mathrm{for}\:{x}\:\Rightarrow \\ $$$${x}=−\frac{{p}^{\mathrm{2}} −\mathrm{6}{p}−\mathrm{1}}{\mathrm{3}{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{inserting}\:\mathrm{and}\:\mathrm{transforming}\:\Rightarrow \\ $$$${p}^{\mathrm{6}} −\frac{\mathrm{135}}{\mathrm{26}}{p}^{\mathrm{5}} −\frac{\mathrm{159}}{\mathrm{26}}{p}^{\mathrm{4}} +\frac{\mathrm{9}}{\mathrm{13}}{p}^{\mathrm{3}} +\frac{\mathrm{12}}{\mathrm{13}}{p}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{26}}{p}+\frac{\mathrm{1}}{\mathrm{26}}=\mathrm{0} \\ $$$$\left({p}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} −\mathrm{6}{p}−\mathrm{1}\right)\left({p}^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{13}}{p}+\frac{\mathrm{1}}{\mathrm{13}}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${p}=−\mathrm{1}\:\Rightarrow\:{x}=\mathrm{1}\wedge{y}=−\mathrm{1}\:\bigstar \\ $$$${p}=\mathrm{3}−\sqrt{\mathrm{10}}\:\Rightarrow\:{x}={y}=\mathrm{0}\:\mathrm{impossible} \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{x}=\mathrm{2}\wedge{y}=\mathrm{1}\:\bigstar \\ $$$${p}=\mathrm{3}+\sqrt{\mathrm{10}}\:\Rightarrow\:{x}={y}=\mathrm{0}\:\mathrm{impossible} \\ $$$${p}=−\frac{\mathrm{2}}{\mathrm{13}}+\frac{\mathrm{3}}{\mathrm{13}}\mathrm{i}\:\Rightarrow\:{x}=\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{i}\wedge{y}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}\:\bigstar \\ $$$${p}=−\frac{\mathrm{2}}{\mathrm{13}}−\frac{\mathrm{3}}{\mathrm{13i}}\:\Rightarrow\:{x}=\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{i}\wedge{y}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}\:\bigstar \\ $$
