
Question Number 152795 by mnjuly1970 last updated on 01/Sep/21
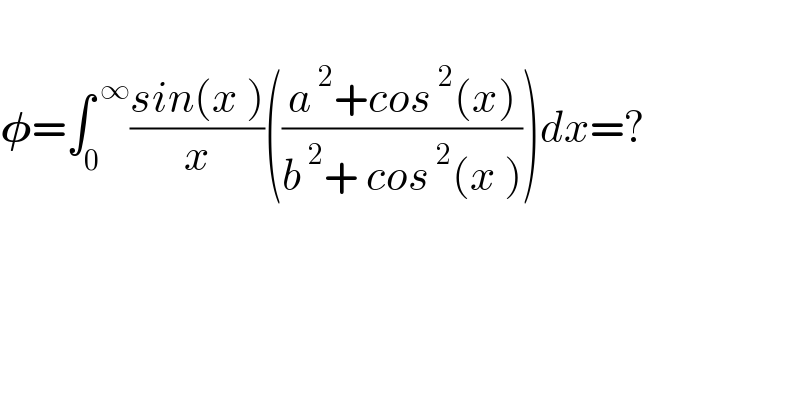
$$ \\ $$$$\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\:\right)}{{x}}\left(\frac{{a}^{\:\mathrm{2}} +{cos}^{\:\mathrm{2}} \left({x}\right)}{{b}^{\:\mathrm{2}} +\:{cos}^{\:\mathrm{2}} \left({x}\:\right)}\right){dx}=? \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 01/Sep/21
![φ = ∫_0 ^∞ ((sinx)/x)(((a^2 +cos^2 x)/(b^2 +cos^2 x))) dx Let f(x) = ((a^2 +cos^2 x)/(b^2 +cos^2 x)) f is a π−periodic function. We can apply the Lobatchevsky−Dirichlet integral formula : φ = ∫_0 ^∞ ((sinx)/x)f(x) dx = ∫_0 ^(π/2) f(x) dx φ = ∫_0 ^(π/2) ((a^2 +cos^2 x)/(b^2 +cos^2 x)) dx φ = ∫_0 ^(π/2) (1+((a^2 −b^2 )/(b^2 +cos^2 x))) dx Let t = tan(x/2) : φ = ∫_0 ^1 (1+((a^2 −b^2 )/(b^2 +((1−t^2 )/(1+t^2 ))))) ((2dt)/(1+t^2 )) φ = 2∫_0 ^1 (1+((a^2 −b^2 )/(b^2 +1+(b^2 −1)t^2 ))) dt Let u = (√(∣b^2 −1∣)).t (case b≠1) : φ = (2/( (√(∣b^2 −1∣))))∫_0 ^(√(∣b^2 −1∣)) (1+((a^2 −b^2 )/(b^2 +1+u^2 ))) du φ = (2/( (√(∣b^2 −1∣))))[u+(a^2 −b^2 )(1/( (√(b^2 +1))))arctan((u/( (√(b^2 +1)))))]_0 ^(√(∣b^2 −1∣)) φ = 2+2((a^2 −b^2 )/( (√(∣b^4 −1∣))))arctan((√(∣((b^2 −1)/(b^2 +1))∣))) do verify my calculous sir](Q152798.png)
$$\phi\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}\left(\frac{{a}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} {x}}{{b}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} {x}}\right)\:{dx} \\ $$$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\frac{{a}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} {x}}{{b}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} {x}} \\ $$$${f}\:\mathrm{is}\:\mathrm{a}\:\pi−\mathrm{periodic}\:\mathrm{function}.\:\mathrm{We}\:\mathrm{can} \\ $$$$\mathrm{apply}\:\mathrm{the}\:\mathrm{Lobatchevsky}−\mathrm{Dirichlet} \\ $$$$\mathrm{integral}\:\mathrm{formula}\:: \\ $$$$\phi\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}{f}\left({x}\right)\:{dx}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({x}\right)\:{dx} \\ $$$$\phi\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{a}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} {x}}{{b}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} {x}}\:{dx} \\ $$$$\phi\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} {x}}\right)\:{dx} \\ $$$$\mathrm{Let}\:{t}\:=\:\mathrm{tan}\frac{{x}}{\mathrm{2}}\:: \\ $$$$\phi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\right)\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\phi\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{1}+\left({b}^{\mathrm{2}} −\mathrm{1}\right){t}^{\mathrm{2}} }\right)\:{dt} \\ $$$$\mathrm{Let}\:{u}\:=\:\sqrt{\mid{b}^{\mathrm{2}} −\mathrm{1}\mid}.{t}\:\left(\mathrm{case}\:{b}\neq\mathrm{1}\right)\:: \\ $$$$\phi\:=\:\frac{\mathrm{2}}{\:\sqrt{\mid{b}^{\mathrm{2}} −\mathrm{1}\mid}}\int_{\mathrm{0}} ^{\sqrt{\mid{b}^{\mathrm{2}} −\mathrm{1}\mid}} \left(\mathrm{1}+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{1}+{u}^{\mathrm{2}} }\right)\:{du} \\ $$$$\phi\:=\:\frac{\mathrm{2}}{\:\sqrt{\mid{b}^{\mathrm{2}} −\mathrm{1}\mid}}\left[{u}+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\frac{\mathrm{1}}{\:\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}}\mathrm{arctan}\left(\frac{{u}}{\:\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}}\right)\right]_{\mathrm{0}} ^{\sqrt{\mid{b}^{\mathrm{2}} −\mathrm{1}\mid}} \\ $$$$\phi\:=\:\mathrm{2}+\mathrm{2}\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\:\sqrt{\mid{b}^{\mathrm{4}} −\mathrm{1}\mid}}\mathrm{arctan}\left(\sqrt{\mid\frac{{b}^{\mathrm{2}} −\mathrm{1}}{{b}^{\mathrm{2}} +\mathrm{1}}\mid}\right) \\ $$$$\boldsymbol{\mathrm{do}}\:\boldsymbol{\mathrm{verify}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{calculous}}\:\boldsymbol{\mathrm{sir}} \\ $$
Commented by SANOGO last updated on 01/Sep/21
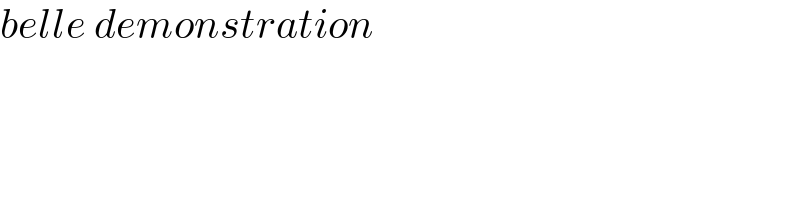
$${belle}\:{demonstration} \\ $$
Commented by mnjuly1970 last updated on 01/Sep/21

$${bravo}\:{sir}\:{olaf} \\ $$
