
Question Number 152753 by mathdanisur last updated on 01/Sep/21
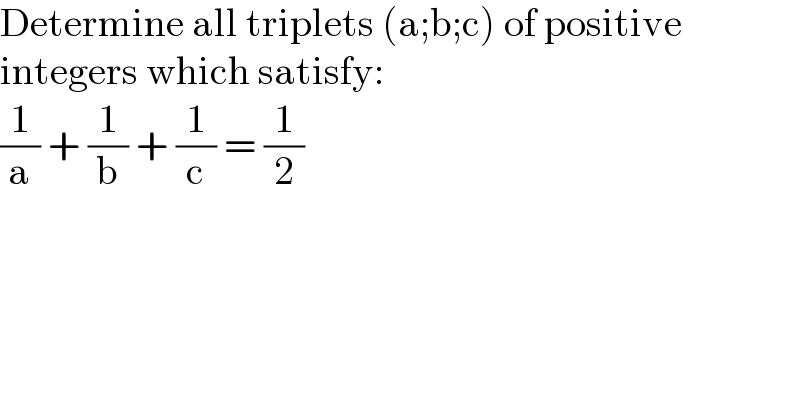
$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{triplets}\:\left(\mathrm{a};\mathrm{b};\mathrm{c}\right)\:\mathrm{of}\:\mathrm{positive} \\ $$$$\mathrm{integers}\:\mathrm{which}\:\mathrm{satisfy}: \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}\:+\:\frac{\mathrm{1}}{\mathrm{c}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Sep/21

$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{triplets}\:\left(\mathrm{a};\mathrm{b};\mathrm{c}\right)\:\mathrm{of}\:\mathrm{positive} \\ $$$$\mathrm{integers}\:\mathrm{which}\:\mathrm{satisfy}: \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}\:+\:\frac{\mathrm{1}}{\mathrm{c}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\bullet\mathrm{C1}:\mathrm{a}=\mathrm{b}=\mathrm{c} \\ $$$$\:\:\:\:\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{k}\left(\mathrm{say}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{k}}+\frac{\mathrm{1}}{\mathrm{k}}+\frac{\mathrm{1}}{\mathrm{k}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}}{\mathrm{k}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{k}=\mathrm{6} \\ $$$$\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{6} \\ $$$$\bullet\mathrm{C2}:\mathrm{b}=\mathrm{c} \\ $$$$\mathrm{b}=\mathrm{c}=\mathrm{k}\left(\mathrm{say}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{k}}+\frac{\mathrm{1}}{\mathrm{k}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{k}+\mathrm{2a}}{\mathrm{ak}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2k}+\mathrm{4a}=\mathrm{ak} \\ $$$$\mathrm{2}\left(\mathrm{k}+\mathrm{2a}\right)=\mathrm{ak} \\ $$$$\mathrm{2}\mid\mathrm{a}\:\vee\:\mathrm{2}\mid\mathrm{k}\:\vee\:\left(\mathrm{2}\mid\mathrm{a}\:\wedge\:\mathrm{2}\mid\mathrm{k}\right) \\ $$$$\bigstar\:\underline{\mathrm{2}\mid\mathrm{a}\:\vee\:\mathrm{2}\mid\mathrm{k}\:\vee\:\left(\mathrm{2}\mid\mathrm{a}\:\wedge\:\mathrm{2}\mid\mathrm{k}\right):} \\ $$$${Let}\:\mathrm{a}=\mathrm{2m} \\ $$$$\mathrm{2}\left(\mathrm{k}+\mathrm{2a}\right)=\mathrm{ak}\Rightarrow\mathrm{2}\left(\mathrm{k}+\mathrm{2}\left(\mathrm{2m}\right)\right)=\left(\mathrm{2m}\right)\mathrm{k} \\ $$$$\mathrm{2}\left(\mathrm{k}+\mathrm{4m}\right)=\mathrm{2mk} \\ $$$$\mathrm{k}+\mathrm{4m}=\mathrm{mk} \\ $$$$\mathrm{m}=\frac{\mathrm{k}}{\mathrm{k}−\mathrm{4}} \\ $$$$\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:\mathrm{k}\:\mathrm{for}\:\mathrm{which}\:\mathrm{m}\in\mathbb{Z}^{+} \\ $$$$\mathrm{k}=\mathrm{5},\mathrm{6},\mathrm{8}\Rightarrow\mathrm{m}=\mathrm{5},\mathrm{3},\mathrm{2} \\ $$$$\mathrm{b}=\mathrm{c}=\mathrm{k}=\mathrm{5}\Rightarrow\mathrm{a}=\mathrm{2m}=\mathrm{10} \\ $$$$\mathrm{b}=\mathrm{c}=\mathrm{k}=\mathrm{6}\Rightarrow\mathrm{a}=\mathrm{2m}=\mathrm{6} \\ $$$$\mathrm{b}=\mathrm{c}=\mathrm{k}=\mathrm{8}\Rightarrow\mathrm{a}=\mathrm{2m}=\mathrm{4} \\ $$$${o}\:\bigstar\underline{\:\mathrm{2}\mid\mathrm{a}\:\vee\:\mathrm{2}\mid\mathrm{k}\:\vee\:\left(\mathrm{2}\mid\mathrm{a}\:\wedge\:\mathrm{2}\mid\mathrm{k}\right):} \\ $$$$\mathrm{k}=\mathrm{2m} \\ $$$$\mathrm{2}\left(\mathrm{k}+\mathrm{2a}\right)=\mathrm{ak}\Rightarrow\mathrm{2}\left(\mathrm{2m}+\mathrm{2a}\right)=\mathrm{2ma} \\ $$$$\:\:\:\:\:\underset{\left(\mathrm{m}\:\mathrm{or}\:\mathrm{a}\:\in\mathbb{E}^{+} \right)} {\mathrm{2m}+\mathrm{2a}=\mathrm{ma}} \\ $$$$\:\:\:\:\:\mathrm{a}=\frac{\mathrm{2m}}{\mathrm{m}−\mathrm{2}} \\ $$$$\mathrm{possible}\:\mathrm{positive}\:\mathrm{integral}\:\mathrm{values}\:\mathrm{of}\:\mathrm{m} \\ $$$$\mathrm{for}\:\mathrm{which}\:\mathrm{a}\:\mathrm{is}\:\mathrm{also}\:\mathrm{positive}\:\mathrm{integer}. \\ $$$$\mathrm{m}=\mathrm{3},\mathrm{4},\mathrm{6}\Rightarrow\mathrm{a}=\mathrm{6},\mathrm{4},\mathrm{3} \\ $$$$\mathrm{b}=\mathrm{c}=\mathrm{k}=\mathrm{2m}=\mathrm{6},\mathrm{8},\mathrm{12} \\ $$$$\left(\mathrm{6},\mathrm{6},\mathrm{6}\right),\left(\mathrm{4},\mathrm{8},\mathrm{8}\right),\left(\mathrm{3},\mathrm{12},\mathrm{12}\right) \\ $$$$\left\{\mathrm{a},\mathrm{b},\mathrm{c}\right\} \\ $$$$=\left\{\mathrm{3},\mathrm{12},\mathrm{12}\right\},\left\{\mathrm{4},\mathrm{8},\mathrm{8}\right\},\left\{\mathrm{10},\mathrm{5},\mathrm{5}\right\},\left\{\mathrm{6},\mathrm{6},\mathrm{6}\right\} \\ $$$$\:\bigstar\underline{\:\mathrm{2}\mid\mathrm{a}\:\vee\:\mathrm{2}\mid\mathrm{k}\:\vee\:\left(\mathrm{2}\mid\mathrm{a}\:\wedge\:\mathrm{2}\mid\mathrm{k}\right):} \\ $$$$\mathrm{a}=\mathrm{2m},\mathrm{k}=\mathrm{2n} \\ $$$$\mathrm{2}\left(\mathrm{k}+\mathrm{2a}\right)=\mathrm{ak}\Rightarrow\mathrm{2}\left(\mathrm{2n}+\mathrm{2}.\mathrm{2m}\right)=\mathrm{2m}.\mathrm{2n} \\ $$$$\mathrm{4}\left(\mathrm{n}+\mathrm{2m}\right)=\mathrm{4mn} \\ $$$$\mathrm{n}+\mathrm{2m}=\mathrm{mn} \\ $$$$\mathrm{mn}−\mathrm{2m}=\mathrm{n} \\ $$$$\mathrm{m}=\frac{\mathrm{n}}{\mathrm{n}−\mathrm{2}} \\ $$$$\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:\mathrm{n} \\ $$$$\mathrm{n}=\mathrm{3},\mathrm{4}\Rightarrow\mathrm{m}=\mathrm{3},\mathrm{2} \\ $$$$\mathrm{a}=\mathrm{2m}=\mathrm{6},\mathrm{4};\:\mathrm{b}=\mathrm{c}=\mathrm{k}=\mathrm{2n}=\mathrm{6},\mathrm{8} \\ $$$$\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\left(\mathrm{6},\mathrm{6},\mathrm{6}\right),\left(\mathrm{4},\mathrm{8},\mathrm{8}\right) \\ $$$$\left\{\mathrm{a},\mathrm{b},\mathrm{c}\right\} \\ $$$$=\left\{\mathrm{3},\mathrm{12},\mathrm{12}\right\},\left\{\mathrm{4},\mathrm{8},\mathrm{8}\right\},\left\{\mathrm{10},\mathrm{5},\mathrm{5}\right\},\left\{\mathrm{6},\mathrm{6},\mathrm{6}\right\} \\ $$$$\bullet\mathrm{C3}:\:\mathrm{a}\neq\mathrm{b}\neq\mathrm{c}\neq\mathrm{a} \\ $$$$\mathrm{a}=\mathrm{k},\mathrm{b}=\mathrm{pk},\mathrm{c}=\mathrm{qk}\:;\mathrm{p},\mathrm{q}\in\mathbb{Z}^{+} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{k}}+\frac{\mathrm{1}}{\mathrm{pk}}+\frac{\mathrm{1}}{\mathrm{qk}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{p}+\mathrm{q}+\mathrm{pq}}{\mathrm{pqk}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{p}+\mathrm{q}+\mathrm{pq}\right)=\mathrm{pqk} \\ $$$$\mathrm{2}\mid\mathrm{p}:\:\mathrm{p}=\mathrm{2m} \\ $$$$\mathrm{2}\left(\mathrm{2m}+\mathrm{q}+\mathrm{pq}\right)=\left(\mathrm{2m}\right)\mathrm{qk} \\ $$$$\mathrm{2m}+\mathrm{q}+\mathrm{2mq}=\mathrm{qmk} \\ $$$$\mathrm{2m}\left(\mathrm{1}+\mathrm{q}\right)=\mathrm{qmk}−\mathrm{q} \\ $$$$\mathrm{2m}\left(\mathrm{1}+\mathrm{q}\right)=\mathrm{q}\left(\mathrm{mk}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{q}}{\mathrm{q}+\mathrm{1}}=\frac{\mathrm{2m}}{\mathrm{mk}−\mathrm{1}} \\ $$$$..... \\ $$$$... \\ $$$$\left(\mathrm{6},\mathrm{12},\mathrm{4}\right)... \\ $$$$\mathrm{Continue} \\ $$
Commented by mathdanisur last updated on 02/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thaankyou} \\ $$
Commented by Rasheed.Sindhi last updated on 02/Sep/21
$${Pl}\:{write}\:{all}\:{answers},\:{if}\:{you}\:{have}. \\ $$
Commented by mathdanisur last updated on 02/Sep/21

$$\left(\mathrm{3},\mathrm{7},\mathrm{42}\right);\left(\mathrm{3},\mathrm{8},\mathrm{24}\right);\left(\mathrm{3},\mathrm{9},\mathrm{18}\right);\left(\mathrm{3},\mathrm{10},\mathrm{15}\right) \\ $$$$\left(\mathrm{3},\mathrm{42},\mathrm{12}\right);\left(\mathrm{4},\mathrm{5},\mathrm{20}\right);\left(\mathrm{4},\mathrm{6},\mathrm{12}\right);\left(\mathrm{4},\mathrm{8},\mathrm{8}\right) \\ $$$$\left(\mathrm{5},\mathrm{5},\mathrm{10}\right);\left(\mathrm{6},\mathrm{6},\mathrm{6}\right)\:\mathrm{and}\:\mathrm{permutations} \\ $$
Commented by Rasheed.Sindhi last updated on 02/Sep/21

$$\mathbb{T}\mathrm{han}\Bbbk\:\mathbb{Y}\mathrm{o}\Cup\:\mathbb{S} \mathrm{r}! \\ $$
Commented by Rasheed.Sindhi last updated on 02/Sep/21
$${mathdanisur}\:{ser},\:{are}\:{you}\:{studying}? \\ $$
Commented by mathdanisur last updated on 02/Sep/21
$$\mathrm{Yes}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{I}\:\mathrm{will}\:\mathrm{finish}\:\mathrm{the}\:\mathrm{highest}\:\mathrm{level} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Sep/21

$${Ser},{Why}\:\:{don}'{t}\:{you}\:{try}\:{to}\:{solve} \\ $$$${any}\:{question}\:{in}\:{this}\:{forum}?\left({Although}\right. \\ $$$${you}\:{have}\:{given}\:{answers}\:{to}\:{some} \\ $$$$\left.{questions}\:{but}\:{not}\:{complete}\:{solutions}?\right) \\ $$
Commented by mathdanisur last updated on 03/Sep/21

$$\mathrm{I}'\mathrm{ve}\:\mathrm{solved},\:\mathrm{well},\:\mathrm{I}\:\mathrm{know}\:\mathrm{the}\:\mathrm{solution} \\ $$$$\mathrm{to}\:\mathrm{most}\:\mathrm{of}\:\mathrm{the}\:\mathrm{questions}\:\mathrm{I}\:\mathrm{sak},\:\mathrm{I}\:\mathrm{just} \\ $$$$\mathrm{want}\:\mathrm{different}\:\mathrm{solutions},\:\mathrm{I}'\mathrm{m}\:\mathrm{learning}, \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{beautiful}\:\mathrm{place},\:\mathrm{there}\:\mathrm{are}\:\mathrm{educated} \\ $$$$\mathrm{people}\:\left(\mathrm{like}\:\mathrm{you}\right)\:\mathrm{and}\:\mathrm{I}\:\mathrm{like}\:\mathrm{your}\:\mathrm{solutions}, \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{for}\:\mathrm{your}\:\mathrm{solutions}... \\ $$
Commented by Rasheed.Sindhi last updated on 03/Sep/21

$$\:^{\bullet} \mathrm{Th}\propto\mathrm{nk}\:\mathrm{You}\:\mathrm{very}\:\mathrm{much}! \\ $$$$\:^{\bullet} \mathrm{Your}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{seems}\:\mathrm{incorrect}: \\ $$$$\:\:\:\left(\mathrm{3},\mathrm{42},\mathrm{12}\right).\mathrm{Pl}\:\mathrm{correct}\:\mathrm{it}. \\ $$$$\:^{\bullet} \mathrm{I}\:\mathrm{wish}\:\mathrm{you}\:\mathrm{share}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{for} \\ $$$$\mathrm{this}\:\mathrm{question}\:\mathrm{because}\:\mathrm{my}\:\mathrm{solutions} \\ $$$$\mathrm{are}\:\mathrm{not}\:\mathrm{fine}\:\mathrm{enough}. \\ $$$$\:\:^{\bullet} \mathrm{Others}\:\mathrm{also}\:\mathrm{want}\:\mathrm{variety}\:\mathrm{in}\:\mathrm{solutions} \\ $$$$\:\mathrm{so}\:\mathrm{if}\:\mathrm{you}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{some} \\ $$$$\:\mathrm{questions}\:\mathrm{pl}\:\mathrm{share}\:\mathrm{their} \\ $$$$\mathrm{solutions}.\left(\mathrm{Particularly}\:\mathrm{solution}\:\mathrm{for}\right. \\ $$$$\left.\mathrm{this}\:\mathrm{question}.\right) \\ $$
Commented by mathdanisur last updated on 03/Sep/21

$$\mathrm{Good}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you},\:\mathrm{sorry}\:\left(\mathrm{3},\mathrm{12},\mathrm{12}\right) \\ $$
Commented by peter frank last updated on 03/Sep/21
$$\mathrm{your}\:\mathrm{selfish}\:\mathrm{if}\:\mathrm{you}\:\mathrm{have}\:\mathrm{soln}\:\mathrm{then} \\ $$$$\mathrm{you}\:\mathrm{dont}\:\mathrm{what}\:\mathrm{to}\:\mathrm{share}\:\mathrm{it}\:\mathrm{this} \\ $$$$\mathrm{not}\:\mathrm{good}\: \\ $$
Answered by Rasheed.Sindhi last updated on 01/Sep/21
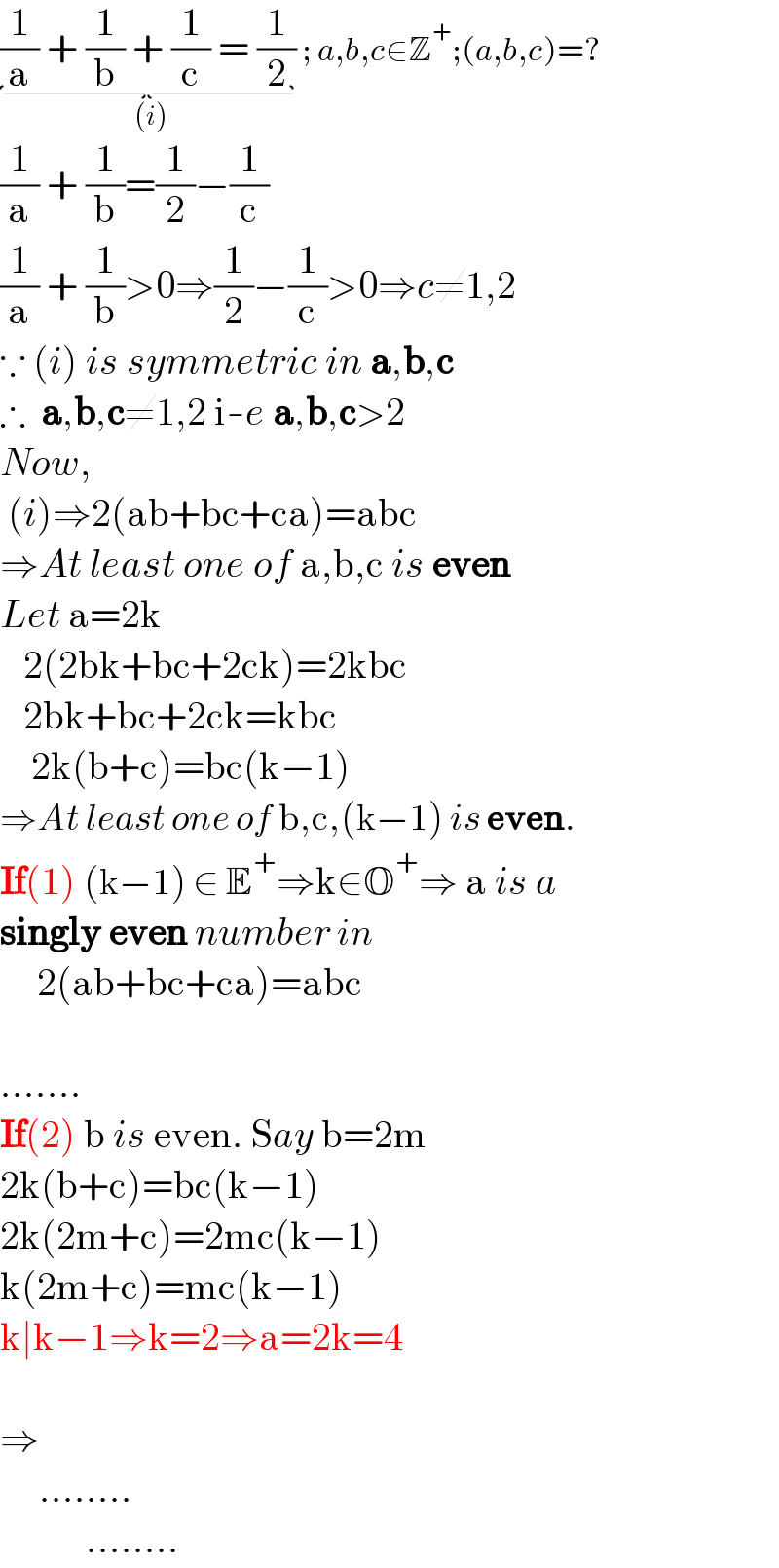
$$\underset{\left({i}\right)} {\underbrace{\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}\:+\:\frac{\mathrm{1}}{\mathrm{c}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}}\:};\:{a},{b},{c}\in\mathbb{Z}^{+} ;\left({a},{b},{c}\right)=? \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{c}} \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}>\mathrm{0}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{c}}>\mathrm{0}\Rightarrow{c}\neq\mathrm{1},\mathrm{2} \\ $$$$\because\:\left({i}\right)\:{is}\:{symmetric}\:{in}\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}} \\ $$$$\therefore\:\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\neq\mathrm{1},\mathrm{2}\:\mathrm{i}-{e}\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}>\mathrm{2} \\ $$$${Now}, \\ $$$$\:\left({i}\right)\Rightarrow\mathrm{2}\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)=\mathrm{abc} \\ $$$$\Rightarrow{At}\:{least}\:{one}\:{of}\:\mathrm{a},\mathrm{b},\mathrm{c}\:{is}\:\boldsymbol{\mathrm{even}} \\ $$$${Let}\:\mathrm{a}=\mathrm{2k} \\ $$$$\:\:\:\mathrm{2}\left(\mathrm{2bk}+\mathrm{bc}+\mathrm{2ck}\right)=\mathrm{2kbc} \\ $$$$\:\:\:\mathrm{2bk}+\mathrm{bc}+\mathrm{2ck}=\mathrm{kbc} \\ $$$$\:\:\:\:\mathrm{2k}\left(\mathrm{b}+\mathrm{c}\right)=\mathrm{bc}\left(\mathrm{k}−\mathrm{1}\right) \\ $$$$\Rightarrow{At}\:{least}\:{one}\:{of}\:\mathrm{b},\mathrm{c},\left(\mathrm{k}−\mathrm{1}\right)\:{is}\:\boldsymbol{\mathrm{even}}. \\ $$$$\boldsymbol{\mathrm{If}}\left(\mathrm{1}\right)\:\left(\mathrm{k}−\mathrm{1}\right)\:\in\:\mathbb{E}^{+} \Rightarrow\mathrm{k}\in\mathbb{O}^{+} \Rightarrow\:\mathrm{a}\:{is}\:{a} \\ $$$$\boldsymbol{\mathrm{singly}}\:\boldsymbol{\mathrm{even}}\:{number}\:{in} \\ $$$$\:\:\:\:\:\:\mathrm{2}\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)=\mathrm{abc} \\ $$$$\: \\ $$$$....... \\ $$$$\boldsymbol{\mathrm{If}}\left(\mathrm{2}\right)\:\mathrm{b}\:{is}\:\mathrm{even}.\:\mathrm{S}{ay}\:\mathrm{b}=\mathrm{2m} \\ $$$$\mathrm{2k}\left(\mathrm{b}+\mathrm{c}\right)=\mathrm{bc}\left(\mathrm{k}−\mathrm{1}\right) \\ $$$$\mathrm{2k}\left(\mathrm{2m}+\mathrm{c}\right)=\mathrm{2mc}\left(\mathrm{k}−\mathrm{1}\right) \\ $$$$\mathrm{k}\left(\mathrm{2m}+\mathrm{c}\right)=\mathrm{mc}\left(\mathrm{k}−\mathrm{1}\right) \\ $$$$\mathrm{k}\mid\mathrm{k}−\mathrm{1}\Rightarrow\mathrm{k}=\mathrm{2}\Rightarrow\mathrm{a}=\mathrm{2k}=\mathrm{4} \\ $$$$ \\ $$$$\Rightarrow \\ $$$$\:\:\:\:\:........ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:........ \\ $$
Commented by mathdanisur last updated on 02/Sep/21

$$\mathrm{Nice}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Rasheed.Sindhi last updated on 03/Sep/21
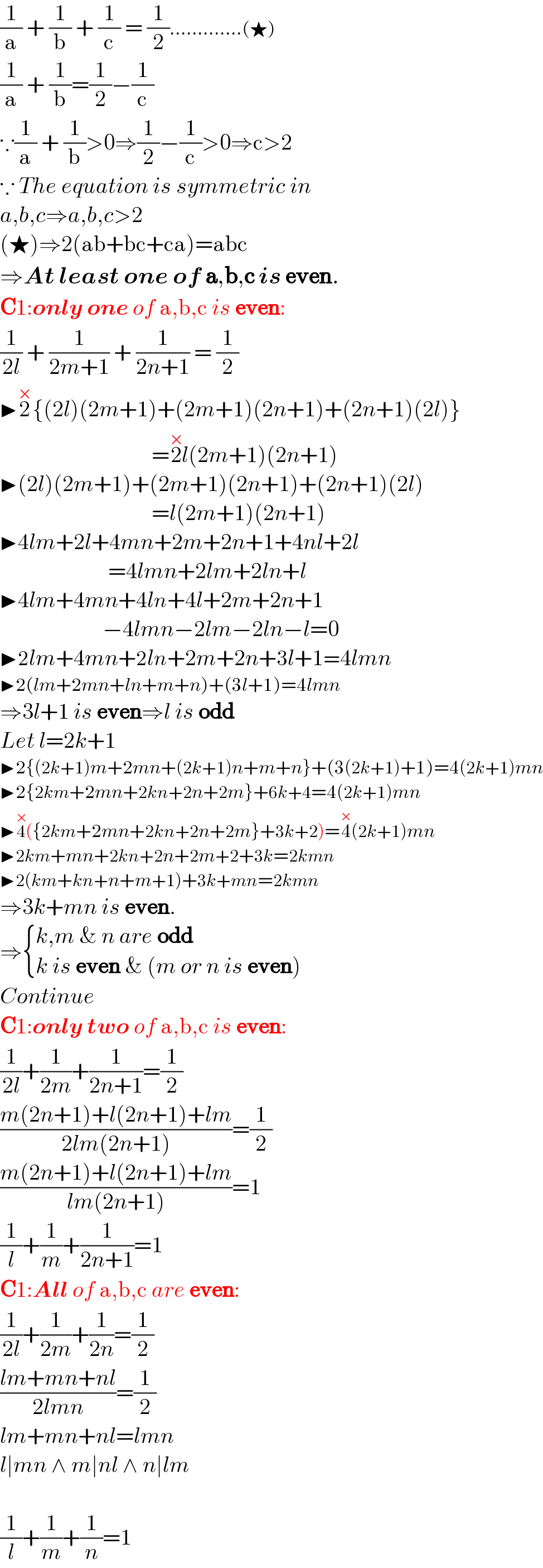
$$\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}\:+\:\frac{\mathrm{1}}{\mathrm{c}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}.............\left(\bigstar\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{c}} \\ $$$$\because\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}>\mathrm{0}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{c}}>\mathrm{0}\Rightarrow\mathrm{c}>\mathrm{2} \\ $$$$\because\:{The}\:{equation}\:{is}\:{symmetric}\:{in} \\ $$$${a},{b},{c}\Rightarrow{a},{b},{c}>\mathrm{2} \\ $$$$\left(\bigstar\right)\Rightarrow\mathrm{2}\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)=\mathrm{abc} \\ $$$$\Rightarrow\boldsymbol{{At}}\:\boldsymbol{{least}}\:\boldsymbol{{one}}\:\boldsymbol{{of}}\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\:\boldsymbol{{is}}\:\boldsymbol{\mathrm{even}}. \\ $$$$\boldsymbol{\mathrm{C}}\mathrm{1}:\boldsymbol{{only}}\:\boldsymbol{{one}}\:{of}\:\mathrm{a},\mathrm{b},\mathrm{c}\:{is}\:\boldsymbol{\mathrm{even}}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{l}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{m}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\blacktriangleright\overset{×} {\mathrm{2}}\left\{\left(\mathrm{2}{l}\right)\left(\mathrm{2}{m}+\mathrm{1}\right)+\left(\mathrm{2}{m}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)+\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{l}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\overset{×} {\mathrm{2}}{l}\left(\mathrm{2}{m}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\blacktriangleright\left(\mathrm{2}{l}\right)\left(\mathrm{2}{m}+\mathrm{1}\right)+\left(\mathrm{2}{m}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)+\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{l}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={l}\left(\mathrm{2}{m}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\blacktriangleright\mathrm{4}{lm}+\mathrm{2}{l}+\mathrm{4}{mn}+\mathrm{2}{m}+\mathrm{2}{n}+\mathrm{1}+\mathrm{4}{nl}+\mathrm{2}{l} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}{lmn}+\mathrm{2}{lm}+\mathrm{2}{ln}+{l} \\ $$$$\blacktriangleright\mathrm{4}{lm}+\mathrm{4}{mn}+\mathrm{4}{ln}+\mathrm{4}{l}+\mathrm{2}{m}+\mathrm{2}{n}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}{lmn}−\mathrm{2}{lm}−\mathrm{2}{ln}−{l}=\mathrm{0} \\ $$$$\blacktriangleright\mathrm{2}{lm}+\mathrm{4}{mn}+\mathrm{2}{ln}+\mathrm{2}{m}+\mathrm{2}{n}+\mathrm{3}{l}+\mathrm{1}=\mathrm{4}{lmn} \\ $$$$\blacktriangleright\mathrm{2}\left({lm}+\mathrm{2}{mn}+{ln}+{m}+{n}\right)+\left(\mathrm{3}{l}+\mathrm{1}\right)=\mathrm{4}{lmn} \\ $$$$\Rightarrow\mathrm{3}{l}+\mathrm{1}\:{is}\:\boldsymbol{\mathrm{even}}\Rightarrow{l}\:{is}\:\boldsymbol{\mathrm{odd}} \\ $$$${Let}\:{l}=\mathrm{2}{k}+\mathrm{1} \\ $$$$\blacktriangleright\mathrm{2}\left\{\left(\mathrm{2}{k}+\mathrm{1}\right){m}+\mathrm{2}{mn}+\left(\mathrm{2}{k}+\mathrm{1}\right){n}+{m}+{n}\right\}+\left(\mathrm{3}\left(\mathrm{2}{k}+\mathrm{1}\right)+\mathrm{1}\right)=\mathrm{4}\left(\mathrm{2}{k}+\mathrm{1}\right){mn} \\ $$$$\blacktriangleright\mathrm{2}\left\{\mathrm{2}{km}+\mathrm{2}{mn}+\mathrm{2}{kn}+\mathrm{2}{n}+\mathrm{2}{m}\right\}+\mathrm{6}{k}+\mathrm{4}=\mathrm{4}\left(\mathrm{2}{k}+\mathrm{1}\right){mn} \\ $$$$\blacktriangleright\overset{×} {\mathrm{4}}\left(\left\{\mathrm{2}{km}+\mathrm{2}{mn}+\mathrm{2}{kn}+\mathrm{2}{n}+\mathrm{2}{m}\right\}+\mathrm{3}{k}+\mathrm{2}\right)=\overset{×} {\mathrm{4}}\left(\mathrm{2}{k}+\mathrm{1}\right){mn} \\ $$$$\blacktriangleright\mathrm{2}{km}+{mn}+\mathrm{2}{kn}+\mathrm{2}{n}+\mathrm{2}{m}+\mathrm{2}+\mathrm{3}{k}=\mathrm{2}{kmn} \\ $$$$\blacktriangleright\mathrm{2}\left({km}+{kn}+{n}+{m}+\mathrm{1}\right)+\mathrm{3}{k}+{mn}=\mathrm{2}{kmn} \\ $$$$\Rightarrow\mathrm{3}{k}+{mn}\:{is}\:\boldsymbol{\mathrm{even}}. \\ $$$$\Rightarrow\begin{cases}{{k},{m}\:\&\:{n}\:{are}\:\boldsymbol{\mathrm{odd}}}\\{{k}\:{is}\:\boldsymbol{\mathrm{even}}\:\&\:\left({m}\:{or}\:{n}\:{is}\:\boldsymbol{\mathrm{even}}\right)}\end{cases} \\ $$$${Continue} \\ $$$$\boldsymbol{\mathrm{C}}\mathrm{1}:\boldsymbol{{only}}\:\boldsymbol{{two}}\:{of}\:\mathrm{a},\mathrm{b},\mathrm{c}\:{is}\:\boldsymbol{\mathrm{even}}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{l}}+\frac{\mathrm{1}}{\mathrm{2}{m}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{m}\left(\mathrm{2}{n}+\mathrm{1}\right)+{l}\left(\mathrm{2}{n}+\mathrm{1}\right)+{lm}}{\mathrm{2}{lm}\left(\mathrm{2}{n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{m}\left(\mathrm{2}{n}+\mathrm{1}\right)+{l}\left(\mathrm{2}{n}+\mathrm{1}\right)+{lm}}{{lm}\left(\mathrm{2}{n}+\mathrm{1}\right)}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{l}}+\frac{\mathrm{1}}{{m}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}=\mathrm{1} \\ $$$$\boldsymbol{\mathrm{C}}\mathrm{1}:\boldsymbol{{All}}\:{of}\:\mathrm{a},\mathrm{b},\mathrm{c}\:{are}\:\boldsymbol{\mathrm{even}}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{l}}+\frac{\mathrm{1}}{\mathrm{2}{m}}+\frac{\mathrm{1}}{\mathrm{2}{n}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{lm}+{mn}+{nl}}{\mathrm{2}{lmn}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${lm}+{mn}+{nl}={lmn} \\ $$$${l}\mid{mn}\:\wedge\:{m}\mid{nl}\:\wedge\:{n}\mid{lm} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{l}}+\frac{\mathrm{1}}{{m}}+\frac{\mathrm{1}}{{n}}=\mathrm{1} \\ $$
