
Question Number 152187 by Tawa11 last updated on 26/Aug/21
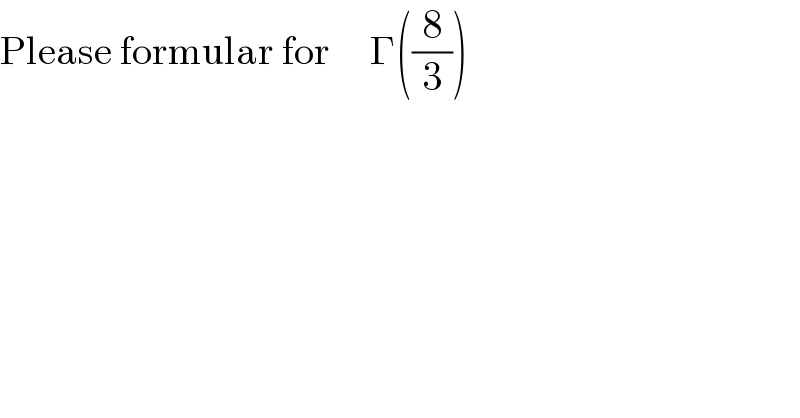
$$\mathrm{Please}\:\mathrm{formular}\:\mathrm{for}\:\:\:\:\:\Gamma\left(\frac{\mathrm{8}}{\mathrm{3}}\right) \\ $$
Commented by Tawa11 last updated on 26/Aug/21
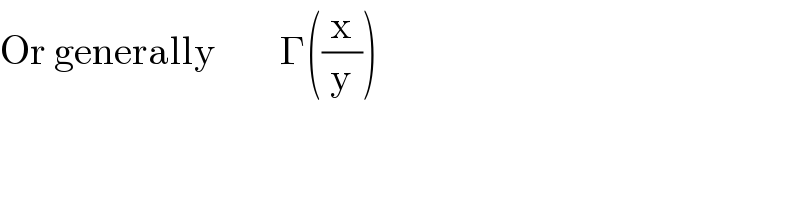
$$\mathrm{Or}\:\mathrm{generally}\:\:\:\:\:\:\:\:\Gamma\left(\frac{\mathrm{x}}{\mathrm{y}}\right) \\ $$
Answered by Olaf_Thorendsen last updated on 26/Aug/21

$$\bullet\:\Gamma\left({z}+\mathrm{1}\right)\:=\:{z}\Gamma\left({z}\right) \\ $$$$\Gamma\left(\frac{\mathrm{8}}{\mathrm{3}}\right)\:=\frac{\mathrm{5}}{\mathrm{3}}\:\Gamma\left(\frac{\mathrm{5}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{5}}{\mathrm{3}}.\frac{\mathrm{2}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{10}}{\mathrm{9}}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$ \\ $$$$\bullet\:\forall{z}\in\mathbb{C}\backslash\mathbb{Z},\:\Gamma\left(\mathrm{1}−{z}\right)\Gamma\left({z}\right)\:=\:\frac{\pi}{\mathrm{sin}\left(\pi{z}\right)} \\ $$$$\bullet\:\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\:\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}\right)} \\ $$$$\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}} \\ $$$$\Gamma\left(\frac{\mathrm{8}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{10}}{\mathrm{9}}.\frac{\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}\:=\:\frac{\mathrm{20}\pi}{\mathrm{9}\sqrt{\mathrm{3}}}.\frac{\mathrm{1}}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{that}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\:\mathrm{3}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}^{\mathrm{3}} } {dt} \\ $$$$\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\approx\:\mathrm{2},\mathrm{678938537} \\ $$$$ \\ $$$$\mathrm{General}\:\mathrm{formula}\:: \\ $$$$\Gamma\left({n}+\frac{\mathrm{1}}{{p}}\right)\:=\:\Gamma\left(\frac{\mathrm{1}}{{p}}\right)\frac{\left({pn}−\left({p}−\mathrm{1}\right)\right)!^{\left({p}\right)} }{{p}^{{n}} } \\ $$$${n}!^{\left({p}\right)} \:\mathrm{denotes}\:\mathrm{the}\:{p}\mathrm{th}\:\mathrm{multifactorial} \\ $$$$\mathrm{of}\:{n}. \\ $$
Commented by Tawa11 last updated on 26/Aug/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
