
Question Number 15207 by arnabpapu550@gmail.com last updated on 08/Jun/17
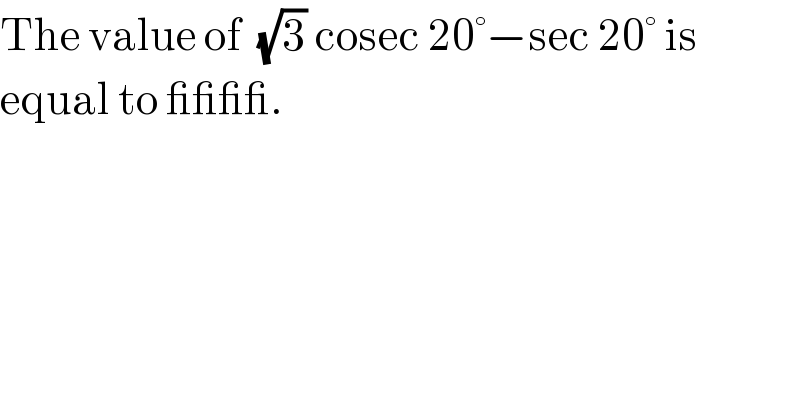
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\:\sqrt{\mathrm{3}}\:\mathrm{cosec}\:\mathrm{20}°−\mathrm{sec}\:\mathrm{20}°\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\_\_\_\_. \\ $$
Answered by mrW1 last updated on 08/Jun/17

$$\frac{\sqrt{\mathrm{3}}}{\mathrm{sin}\:\mathrm{20}°}−\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{20}°}=\frac{\sqrt{\mathrm{3}}\mathrm{cos}\:\mathrm{20}°−\mathrm{sin}\:\mathrm{20}°}{\mathrm{sin}\:\mathrm{20}°\mathrm{cos}\:\mathrm{20}°} \\ $$$$=\frac{\mathrm{4}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\mathrm{20}°−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{20}°\right)}{\mathrm{2sin}\:\mathrm{20}°\mathrm{cos}\:\mathrm{20}°} \\ $$$$=\frac{\mathrm{4}\left(\mathrm{cos}\:\mathrm{30}°\mathrm{cos}\:\mathrm{20}°−\mathrm{sin}\:\mathrm{30}°\mathrm{sin}\:\mathrm{20}°\right)}{\mathrm{sin}\:\mathrm{40}°} \\ $$$$=\frac{\mathrm{4cos}\:\mathrm{50}°}{\mathrm{sin}\:\mathrm{40}°} \\ $$$$=\frac{\mathrm{4sin}\:\mathrm{40}°}{\mathrm{sin}\:\mathrm{40}°} \\ $$$$=\mathrm{4} \\ $$
Commented by arnabpapu550@gmail.com last updated on 08/Jun/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
