
Question Number 150881 by mathdanisur last updated on 16/Aug/21
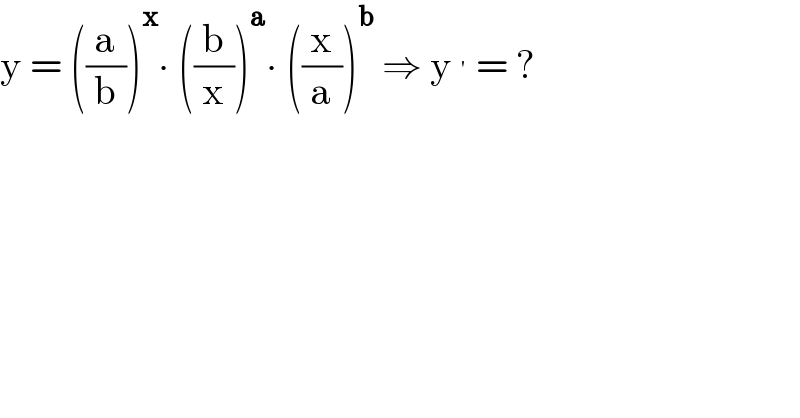
$$\mathrm{y}\:=\:\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\boldsymbol{\mathrm{x}}} \centerdot\:\left(\frac{\mathrm{b}}{\mathrm{x}}\right)^{\boldsymbol{\mathrm{a}}} \centerdot\:\left(\frac{\mathrm{x}}{\mathrm{a}}\right)^{\boldsymbol{\mathrm{b}}} \:\Rightarrow\:\mathrm{y}\:^{'} \:=\:? \\ $$
Answered by john_santu last updated on 16/Aug/21
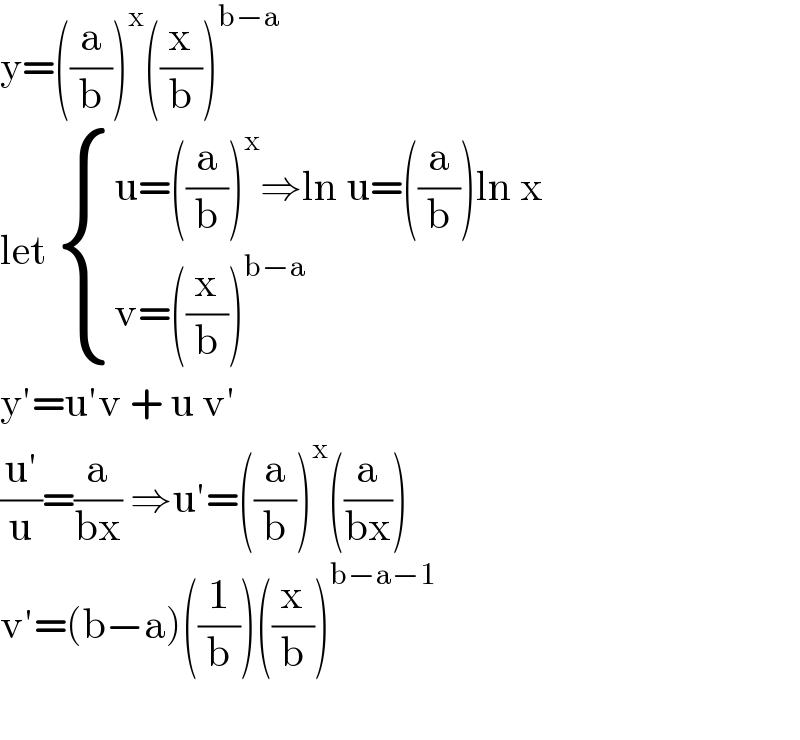
$$\mathrm{y}=\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\mathrm{x}} \left(\frac{\mathrm{x}}{\mathrm{b}}\right)^{\mathrm{b}−\mathrm{a}} \\ $$$$\mathrm{let}\:\begin{cases}{\mathrm{u}=\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\mathrm{x}} \Rightarrow\mathrm{ln}\:\mathrm{u}=\left(\frac{\mathrm{a}}{\mathrm{b}}\right)\mathrm{ln}\:\mathrm{x}}\\{\mathrm{v}=\left(\frac{\mathrm{x}}{\mathrm{b}}\right)^{\mathrm{b}−\mathrm{a}} }\end{cases} \\ $$$$\mathrm{y}'=\mathrm{u}'\mathrm{v}\:+\:\mathrm{u}\:\mathrm{v}' \\ $$$$\frac{\mathrm{u}'}{\mathrm{u}}=\frac{\mathrm{a}}{\mathrm{bx}}\:\Rightarrow\mathrm{u}'=\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\mathrm{x}} \left(\frac{\mathrm{a}}{\mathrm{bx}}\right) \\ $$$$\mathrm{v}'=\left(\mathrm{b}−\mathrm{a}\right)\left(\frac{\mathrm{1}}{\mathrm{b}}\right)\left(\frac{\mathrm{x}}{\mathrm{b}}\right)^{\mathrm{b}−\mathrm{a}−\mathrm{1}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 16/Aug/21
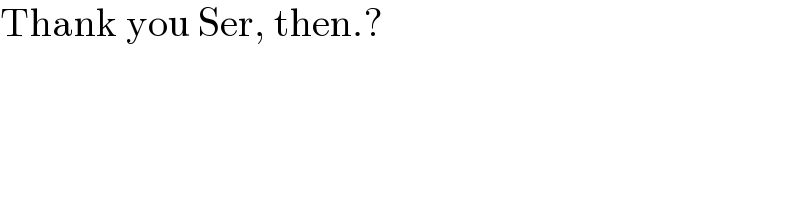
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser},\:\mathrm{then}.? \\ $$
