
Question Number 150683 by Jonathanwaweh last updated on 14/Aug/21

Commented by Tawa11 last updated on 14/Aug/21

$$\mathrm{Great} \\ $$
Answered by ajfour last updated on 14/Aug/21
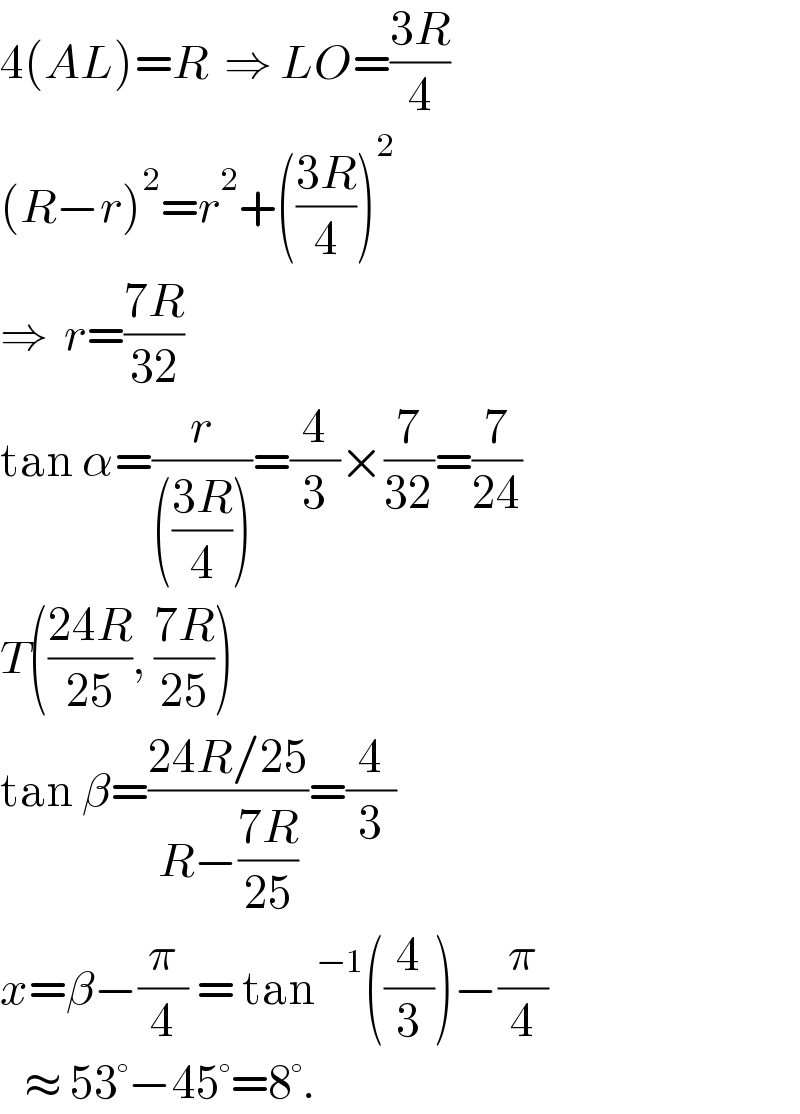
$$\mathrm{4}\left({AL}\right)={R}\:\:\Rightarrow\:{LO}=\frac{\mathrm{3}{R}}{\mathrm{4}} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\left(\frac{\mathrm{3}{R}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{r}=\frac{\mathrm{7}{R}}{\mathrm{32}} \\ $$$$\mathrm{tan}\:\alpha=\frac{{r}}{\left(\frac{\mathrm{3}{R}}{\mathrm{4}}\right)}=\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{7}}{\mathrm{32}}=\frac{\mathrm{7}}{\mathrm{24}} \\ $$$${T}\left(\frac{\mathrm{24}{R}}{\mathrm{25}},\:\frac{\mathrm{7}{R}}{\mathrm{25}}\right) \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{24}{R}/\mathrm{25}}{{R}−\frac{\mathrm{7}{R}}{\mathrm{25}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${x}=\beta−\frac{\pi}{\mathrm{4}}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)−\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\approx\:\mathrm{53}°−\mathrm{45}°=\mathrm{8}°. \\ $$
Commented by mr W last updated on 14/Aug/21
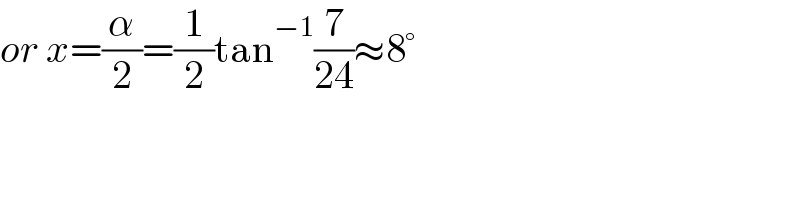
$${or}\:{x}=\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{24}}\approx\mathrm{8}° \\ $$
Commented by mr W last updated on 14/Aug/21
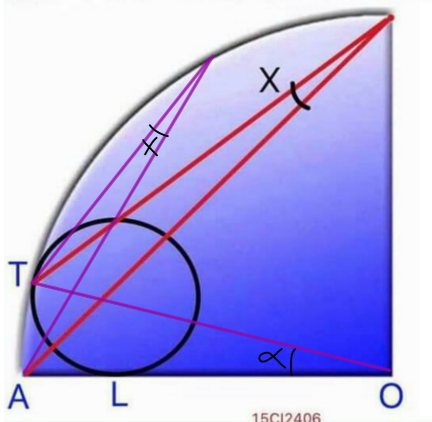
Commented by ajfour last updated on 14/Aug/21
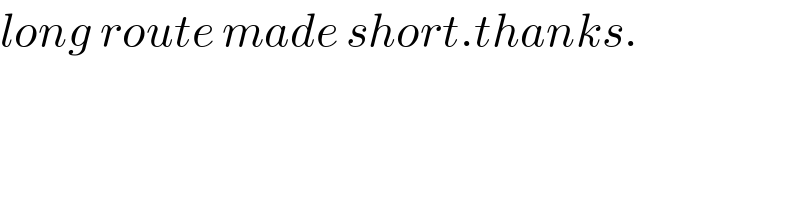
$${long}\:{route}\:{made}\:{short}.{thanks}. \\ $$
