
Question Number 149986 by mnjuly1970 last updated on 08/Aug/21
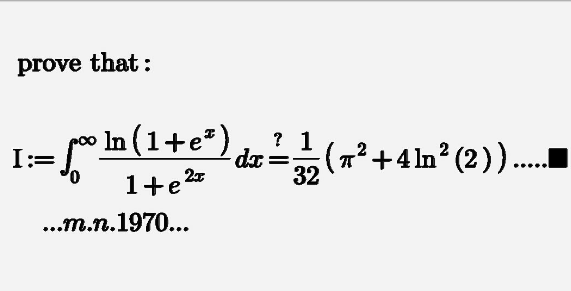
Answered by mindispower last updated on 08/Aug/21

$${ln}\left(\mathrm{1}+{e}^{{x}} \right)={x}+{ln}\left({e}^{−{x}} +\mathrm{1}\right) \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{x}}{\mathrm{1}+{e}^{\mathrm{2}{x}} }{dx}+\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{2}{x}} {ln}\left(\mathrm{1}+{e}^{−{x}} \right)}{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{tdt}}{\mathrm{1}+{e}^{{t}} }+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\Gamma\left(\mathrm{2}\right)\zeta\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{done}\:{with}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+\sqrt{{x}}\right)}{\mathrm{1}+{x}}{dx}\:{Quation}\: \\ $$$$={posted} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 08/Aug/21
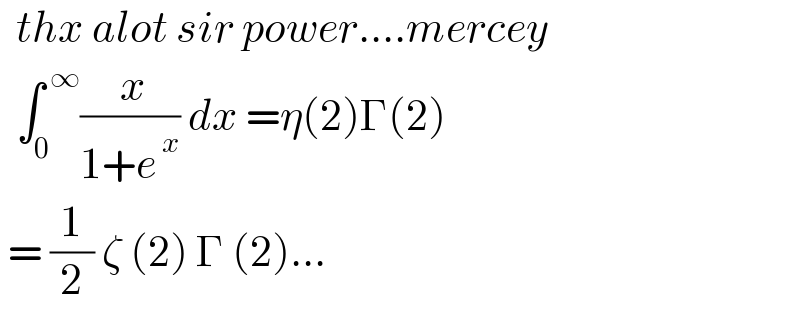
$$\:\:{thx}\:{alot}\:{sir}\:{power}....{mercey} \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{x}}{\mathrm{1}+{e}^{\:{x}} }\:{dx}\:=\eta\left(\mathrm{2}\right)\Gamma\left(\mathrm{2}\right) \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\zeta\:\left(\mathrm{2}\right)\:\Gamma\:\left(\mathrm{2}\right)... \\ $$
