
Question Number 14977 by Tinkutara last updated on 06/Jun/17
![Find the real roots of the equation cos^4 x + sin^7 x = 1 in the interval [−π, π].](Q14977.png)
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{cos}^{\mathrm{4}} \:{x}\:+\:\mathrm{sin}^{\mathrm{7}} \:{x}\:=\:\mathrm{1}\:\mathrm{in}\:\mathrm{the}\:\mathrm{interval}\:\left[−\pi,\:\pi\right]. \\ $$
Commented by mrW1 last updated on 06/Jun/17
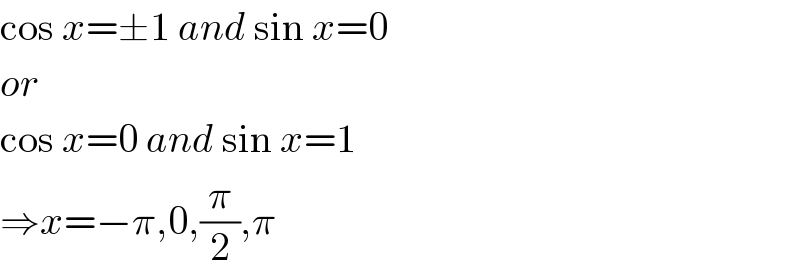
$$\mathrm{cos}\:{x}=\pm\mathrm{1}\:{and}\:\mathrm{sin}\:{x}=\mathrm{0} \\ $$$${or} \\ $$$$\mathrm{cos}\:{x}=\mathrm{0}\:{and}\:\mathrm{sin}\:{x}=\mathrm{1} \\ $$$$\Rightarrow{x}=−\pi,\mathrm{0},\frac{\pi}{\mathrm{2}},\pi \\ $$
Commented by Tinkutara last updated on 07/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by myintkhaing last updated on 07/Jun/17
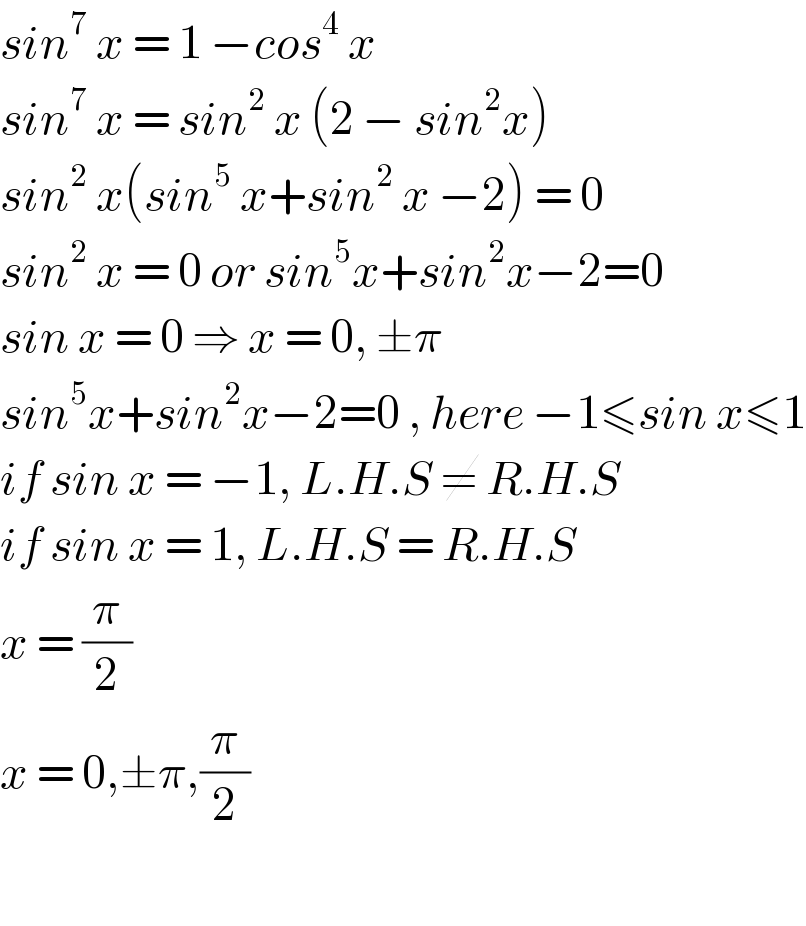
$${sin}^{\mathrm{7}} \:{x}\:=\:\mathrm{1}\:−{cos}^{\mathrm{4}} \:{x} \\ $$$${sin}^{\mathrm{7}} \:{x}\:=\:{sin}^{\mathrm{2}} \:{x}\:\left(\mathrm{2}\:−\:{sin}^{\mathrm{2}} {x}\right) \\ $$$${sin}^{\mathrm{2}} \:{x}\left({sin}^{\mathrm{5}} \:{x}+{sin}^{\mathrm{2}} \:{x}\:−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$${sin}^{\mathrm{2}} \:{x}\:=\:\mathrm{0}\:{or}\:{sin}^{\mathrm{5}} {x}+{sin}^{\mathrm{2}} {x}−\mathrm{2}=\mathrm{0} \\ $$$${sin}\:{x}\:=\:\mathrm{0}\:\Rightarrow\:{x}\:=\:\mathrm{0},\:\pm\pi \\ $$$${sin}^{\mathrm{5}} {x}+{sin}^{\mathrm{2}} {x}−\mathrm{2}=\mathrm{0}\:,\:{here}\:−\mathrm{1}\leqslant{sin}\:{x}\leqslant\mathrm{1} \\ $$$${if}\:{sin}\:{x}\:=\:−\mathrm{1},\:{L}.{H}.{S}\:\neq\:{R}.{H}.{S} \\ $$$${if}\:{sin}\:{x}\:=\:\mathrm{1},\:{L}.{H}.{S}\:=\:{R}.{H}.{S} \\ $$$${x}\:=\:\frac{\pi}{\mathrm{2}} \\ $$$${x}\:=\:\mathrm{0},\pm\pi,\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by Tinkutara last updated on 07/Jun/17
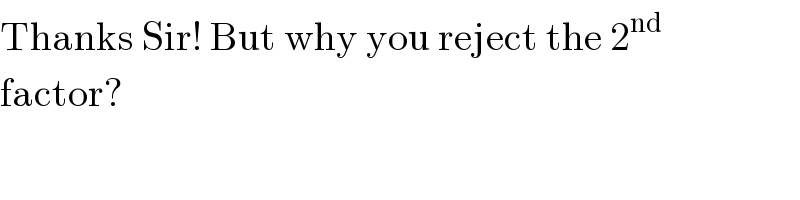
$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{But}\:\mathrm{why}\:\mathrm{you}\:\mathrm{reject}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \\ $$$$\mathrm{factor}? \\ $$
Commented by myintkhaing last updated on 07/Jun/17
$${My}\:{post}\:{is}\:{edited}. \\ $$
Commented by Tinkutara last updated on 07/Jun/17
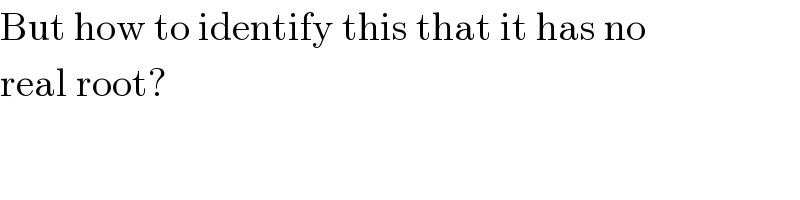
$$\mathrm{But}\:\mathrm{how}\:\mathrm{to}\:\mathrm{identify}\:\mathrm{this}\:\mathrm{that}\:\mathrm{it}\:\mathrm{has}\:\mathrm{no} \\ $$$$\mathrm{real}\:\mathrm{root}? \\ $$
Commented by Tinkutara last updated on 07/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by mrW1 last updated on 07/Jun/17
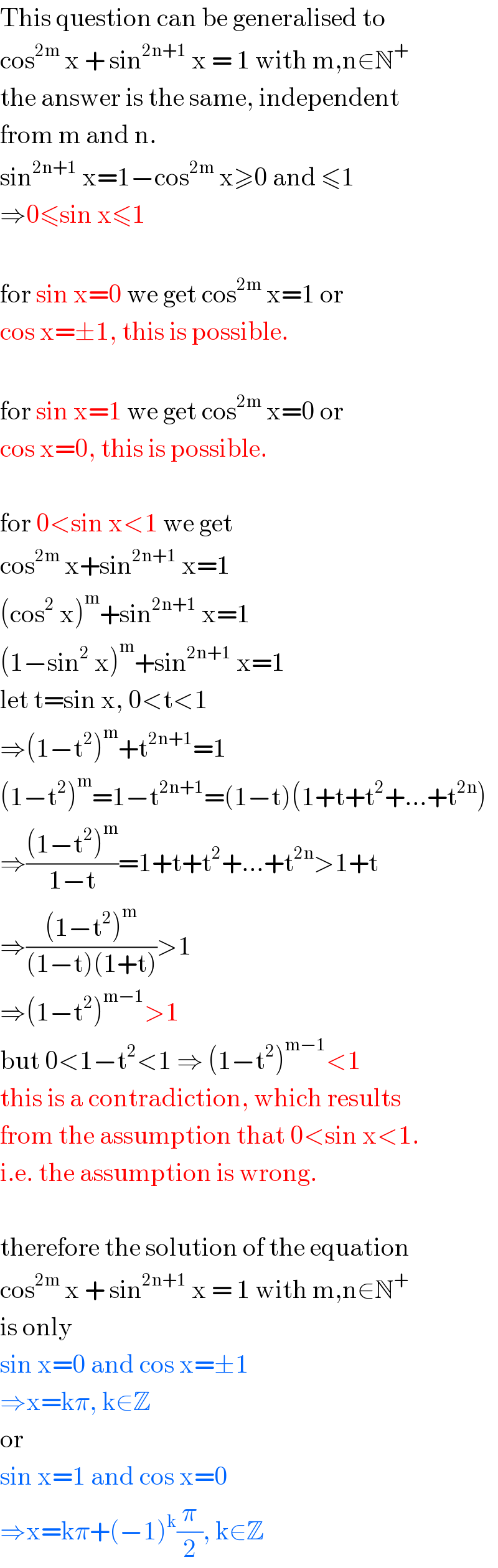
$$\mathrm{This}\:\mathrm{question}\:\mathrm{can}\:\mathrm{be}\:\mathrm{generalised}\:\mathrm{to} \\ $$$$\mathrm{cos}^{\mathrm{2m}} \:\mathrm{x}\:+\:\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{x}\:=\:\mathrm{1}\:\mathrm{with}\:\mathrm{m},\mathrm{n}\in\mathbb{N}^{+} \\ $$$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same},\:\mathrm{independent} \\ $$$$\mathrm{from}\:\mathrm{m}\:\mathrm{and}\:\mathrm{n}. \\ $$$$\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{x}=\mathrm{1}−\mathrm{cos}^{\mathrm{2m}} \:\mathrm{x}\geqslant\mathrm{0}\:\mathrm{and}\:\leqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{0}\leqslant\mathrm{sin}\:\mathrm{x}\leqslant\mathrm{1} \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{sin}\:\mathrm{x}=\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{cos}^{\mathrm{2m}} \:\mathrm{x}=\mathrm{1}\:\mathrm{or} \\ $$$$\mathrm{cos}\:\mathrm{x}=\pm\mathrm{1},\:\mathrm{this}\:\mathrm{is}\:\mathrm{possible}. \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{sin}\:\mathrm{x}=\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:\mathrm{cos}^{\mathrm{2m}} \:\mathrm{x}=\mathrm{0}\:\mathrm{or} \\ $$$$\mathrm{cos}\:\mathrm{x}=\mathrm{0},\:\mathrm{this}\:\mathrm{is}\:\mathrm{possible}. \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{0}<\mathrm{sin}\:\mathrm{x}<\mathrm{1}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{cos}^{\mathrm{2m}} \:\mathrm{x}+\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{x}=\mathrm{1} \\ $$$$\left(\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}\right)^{\mathrm{m}} +\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{x}=\mathrm{1} \\ $$$$\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\mathrm{x}\right)^{\mathrm{m}} +\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{let}\:\mathrm{t}=\mathrm{sin}\:\mathrm{x},\:\mathrm{0}<\mathrm{t}<\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{m}} +\mathrm{t}^{\mathrm{2n}+\mathrm{1}} =\mathrm{1} \\ $$$$\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{m}} =\mathrm{1}−\mathrm{t}^{\mathrm{2n}+\mathrm{1}} =\left(\mathrm{1}−\mathrm{t}\right)\left(\mathrm{1}+\mathrm{t}+\mathrm{t}^{\mathrm{2}} +...+\mathrm{t}^{\mathrm{2n}} \right) \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{m}} }{\mathrm{1}−\mathrm{t}}=\mathrm{1}+\mathrm{t}+\mathrm{t}^{\mathrm{2}} +...+\mathrm{t}^{\mathrm{2n}} >\mathrm{1}+\mathrm{t} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{m}} }{\left(\mathrm{1}−\mathrm{t}\right)\left(\mathrm{1}+\mathrm{t}\right)}>\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{m}−\mathrm{1}} >\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{0}<\mathrm{1}−\mathrm{t}^{\mathrm{2}} <\mathrm{1}\:\Rightarrow\:\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{m}−\mathrm{1}} <\mathrm{1} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{contradiction},\:\mathrm{which}\:\mathrm{results} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{assumption}\:\mathrm{that}\:\mathrm{0}<\mathrm{sin}\:\mathrm{x}<\mathrm{1}. \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{the}\:\mathrm{assumption}\:\mathrm{is}\:\mathrm{wrong}. \\ $$$$ \\ $$$$\mathrm{therefore}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{cos}^{\mathrm{2m}} \:\mathrm{x}\:+\:\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{x}\:=\:\mathrm{1}\:\mathrm{with}\:\mathrm{m},\mathrm{n}\in\mathbb{N}^{+} \\ $$$$\mathrm{is}\:\mathrm{only} \\ $$$$\mathrm{sin}\:\mathrm{x}=\mathrm{0}\:\mathrm{and}\:\mathrm{cos}\:\mathrm{x}=\pm\mathrm{1}\: \\ $$$$\Rightarrow\mathrm{x}=\mathrm{k}\pi,\:\mathrm{k}\in\mathbb{Z} \\ $$$$\mathrm{or} \\ $$$$\mathrm{sin}\:\mathrm{x}=\mathrm{1}\:\mathrm{and}\:\mathrm{cos}\:\mathrm{x}=\mathrm{0}\: \\ $$$$\Rightarrow\mathrm{x}=\mathrm{k}\pi+\left(−\mathrm{1}\right)^{\mathrm{k}} \frac{\pi}{\mathrm{2}},\:\mathrm{k}\in\mathbb{Z} \\ $$
Commented by Tinkutara last updated on 07/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
