
Question Number 149670 by EDWIN88 last updated on 06/Aug/21
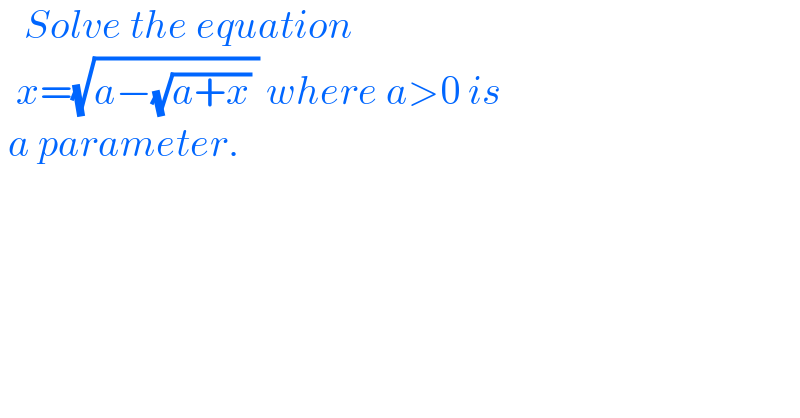
$$\:\:\:{Solve}\:{the}\:{equation}\: \\ $$ $$\:\:{x}=\sqrt{{a}−\sqrt{{a}+{x}}\:}\:{where}\:{a}>\mathrm{0}\:{is}\: \\ $$ $$\:{a}\:{parameter}. \\ $$
Answered by MJS_new last updated on 06/Aug/21

$$\mathrm{for}\:{a},\:{x}\:\in\mathbb{R} \\ $$ $$\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that} \\ $$ $$\mathrm{0}\leqslant{x}\leqslant{a}\left({a}−\mathrm{1}\right) \\ $$ $$\Rightarrow\:{a}\geqslant\mathrm{1} \\ $$ $$ \\ $$ $${x}=\sqrt{{a}−\sqrt{{a}+{x}}} \\ $$ $$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming}\:\mathrm{2}\:\mathrm{times} \\ $$ $$\left(\mathrm{beware}\:\mathrm{of}\:\mathrm{false}\:\mathrm{solutions}!\right) \\ $$ $$\mathrm{leads}\:\mathrm{to} \\ $$ $${a}^{\mathrm{2}} −\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right){a}+{x}\left({x}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{0} \\ $$ $$\Rightarrow \\ $$ $${a}_{\mathrm{1}} ={x}^{\mathrm{2}} −{x}\vee{a}_{\mathrm{2}} ={x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$ $$\mathrm{testing}\:{a}_{\mathrm{1}} : \\ $$ $${x}=\sqrt{{x}^{\mathrm{2}} −{x}−\sqrt{{x}^{\mathrm{2}} −{x}+{x}}} \\ $$ $${x}=\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}}\:\Rightarrow\:{x}=\mathrm{0}\:\Rightarrow\:{a}=\mathrm{0} \\ $$ $$\mathrm{testing}\:{a}_{\mathrm{2}} : \\ $$ $${x}=\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}−\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}+{x}}} \\ $$ $${x}=\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}−\mid{x}+\mathrm{1}\mid} \\ $$ $${x}\geqslant\mathrm{0}\:\Rightarrow\:{x}=\sqrt{{x}^{\mathrm{2}} }\:\mathrm{always}\:\mathrm{true} \\ $$ $$\Rightarrow \\ $$ $${a}={x}^{\mathrm{2}} +{x}+\mathrm{1}\:\Leftrightarrow\:{x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{4}{a}−\mathrm{3}}}{\mathrm{2}} \\ $$ $${x}\geqslant\mathrm{0}\:\Rightarrow \\ $$ $$\bigstar\:{x}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{4}{a}−\mathrm{3}}}{\mathrm{2}}\:\bigstar \\ $$
Commented bymr W last updated on 07/Aug/21

$${great}! \\ $$
