
Question Number 149192 by Samimsultani last updated on 03/Aug/21
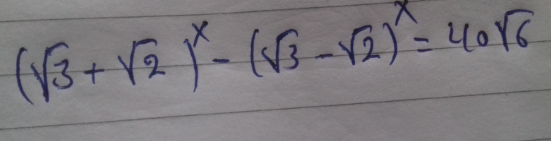
Answered by prakash jain last updated on 03/Aug/21
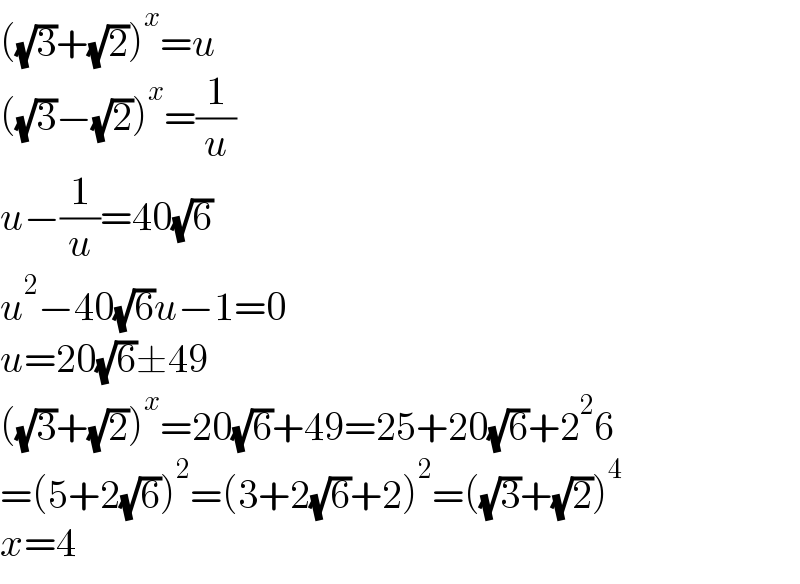
$$\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{{x}} ={u} \\ $$$$\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)^{{x}} =\frac{\mathrm{1}}{{u}} \\ $$$${u}−\frac{\mathrm{1}}{{u}}=\mathrm{40}\sqrt{\mathrm{6}} \\ $$$${u}^{\mathrm{2}} −\mathrm{40}\sqrt{\mathrm{6}}{u}−\mathrm{1}=\mathrm{0} \\ $$$${u}=\mathrm{20}\sqrt{\mathrm{6}}\pm\mathrm{49} \\ $$$$\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{{x}} =\mathrm{20}\sqrt{\mathrm{6}}+\mathrm{49}=\mathrm{25}+\mathrm{20}\sqrt{\mathrm{6}}+\mathrm{2}^{\mathrm{2}} \mathrm{6} \\ $$$$=\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} =\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{6}}+\mathrm{2}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \\ $$$${x}=\mathrm{4} \\ $$
Commented by prakash jain last updated on 03/Aug/21

$$\mathrm{Yes}.\:{x}=\mathrm{4}\:\mathrm{is}\:\mathrm{only}\:\mathrm{correct}\:\mathrm{solution}. \\ $$$$\mathrm{My}\:\mathrm{mistake}. \\ $$$$\mathrm{20}\sqrt{\mathrm{6}}−\mathrm{49}\:\mathrm{does}\:\mathrm{not}\:\mathrm{give}\:\mathrm{any}\:\mathrm{solution} \\ $$
