
Question Number 147978 by mathdanisur last updated on 24/Jul/21
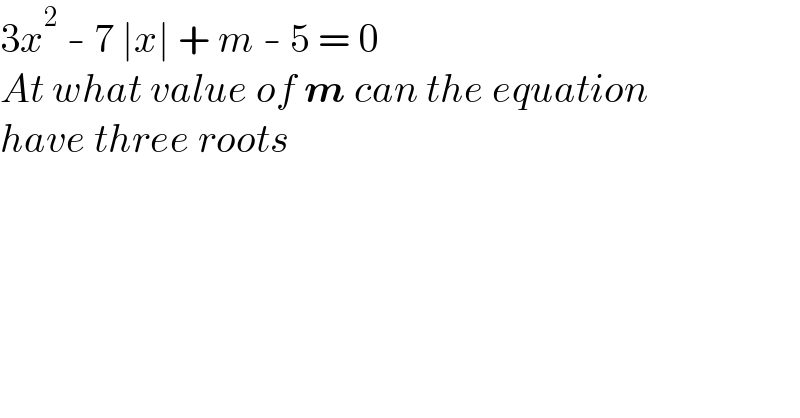
$$\mathrm{3}{x}^{\mathrm{2}} \:-\:\mathrm{7}\:\mid{x}\mid\:+\:{m}\:-\:\mathrm{5}\:=\:\mathrm{0}\: \\ $$$${At}\:{what}\:{value}\:{of}\:\boldsymbol{{m}}\:{can}\:{the}\:{equation} \\ $$$${have}\:{three}\:{roots} \\ $$
Answered by Olaf_Thorendsen last updated on 24/Jul/21

$$\mathrm{In}\:\mathbb{R},\:\mathrm{the}\:\mathrm{equation}\:\mathrm{can}\:\mathrm{have}\:\mathrm{two} \\ $$$$\mathrm{opposite}\:\mathrm{solutions}\:\mathrm{for}\:{x}<\mathrm{0}\:\left(\mid{x}\mid\:=\:−{x}\right) \\ $$$$\mathrm{and}\:\mathrm{two}\:\mathrm{opposite}\:\mathrm{solutions}\:\mathrm{for}\:{x}>\mathrm{0} \\ $$$$\left(\mid{x}\mid\:=\:{x}\right). \\ $$$$ \\ $$$$\mathrm{To}\:\mathrm{obtain}\:\mathrm{exactly}\:\mathrm{three}\:\mathrm{roots},\:\mathrm{one}\:\mathrm{root} \\ $$$$\mathrm{needs}\:\mathrm{to}\:\mathrm{be}\:\mathrm{0}\:\left(\mathrm{to}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{its}\right. \\ $$$$\left.\mathrm{opposite}\right). \\ $$$$\mathrm{That}\:\mathrm{occurs}\:\mathrm{when}\:\frac{{c}}{{a}}\:=\:\frac{{m}−\mathrm{5}}{\mathrm{3}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{m}\:=\:\mathrm{5}. \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case}\:\mathrm{3}{x}^{\mathrm{2}} \:=\:\mathrm{7}\mid{x}\mid \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{0},\:{x}\:=\:\pm\frac{\mathrm{7}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thankyou}\:{Ser} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Jul/21

$$\mathrm{3}{x}^{\mathrm{2}} \:-\:\mathrm{7}\:\mid{x}\mid\:+\:{m}\:-\:\mathrm{5}\:=\:\mathrm{0}\: \\ $$$$\Rightarrow\begin{cases}{{i}:\mathrm{3}{x}^{\mathrm{2}} \:-\:\mathrm{7}{x}\:=−\:{m}\:+\:\mathrm{5}}\\{{ii}:\mathrm{3}{x}^{\mathrm{2}} \:+\:\mathrm{7}{x}=\:−\:{m}\:+\:\mathrm{5}}\end{cases}\Rightarrow\overset{×} {\mathrm{3}{x}^{\mathrm{2}} }−\mathrm{7}{x}=\overset{×} {\mathrm{3}{x}^{\mathrm{2}} }+\mathrm{7}{x} \\ $$$$\Rightarrow{x}=\mathrm{0}\:\left({common}\:{root}\:{of}\:{i}\:\&\:{ii}\right) \\ $$$$\because\:\:{i}\:\:\:\&\:\:\:{ii}\:\:\:\:{have}\:{one}\:{root}\:\:{common} \\ $$$$\therefore\:\mathcal{T}{hey}\:{have}\:{total}\:{three}\:{roots} \\ $$$$\therefore\:\mathcal{T}{he}\:{original}\:{equation}\:{has}\:\mathrm{3}\:{roots} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} \:-\:\mathrm{7}\:\mid{x}\mid\:+\:{m}\:-\:\mathrm{5}\:=\:\mathrm{0}\: \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{7}\mid\mathrm{0}\mid+{m}−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow{m}−\mathrm{5}=\mathrm{0}\Rightarrow{m}=\mathrm{5} \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
