
Question Number 147670 by mnjuly1970 last updated on 22/Jul/21
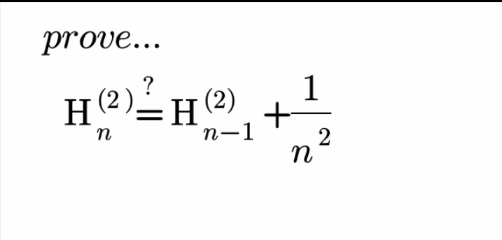
Answered by Olaf_Thorendsen last updated on 22/Jul/21
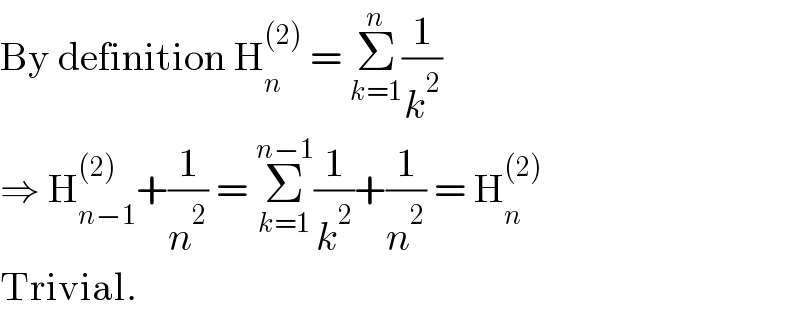
$$\mathrm{By}\:\mathrm{definition}\:\mathrm{H}_{{n}} ^{\left(\mathrm{2}\right)} \:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{H}_{{n}−\mathrm{1}} ^{\left(\mathrm{2}\right)} +\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\:\mathrm{H}_{{n}} ^{\left(\mathrm{2}\right)} \\ $$$$\mathrm{Trivial}. \\ $$
