
Question Number 147581 by EDWIN88 last updated on 22/Jul/21
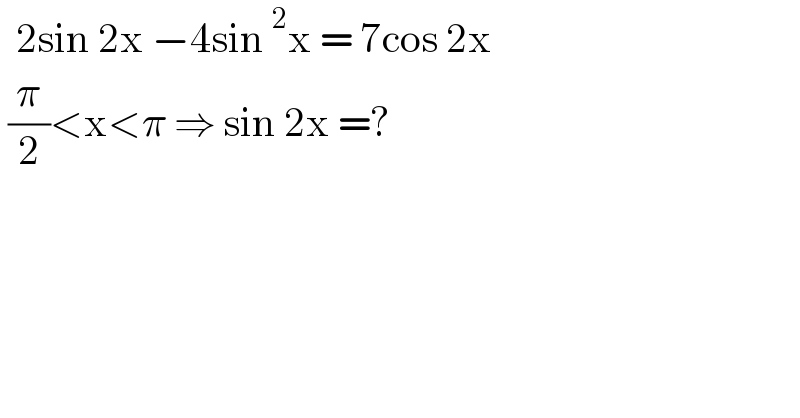
$$\:\:\mathrm{2sin}\:\mathrm{2x}\:−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{7cos}\:\mathrm{2x}\: \\ $$ $$\:\frac{\pi}{\mathrm{2}}<\mathrm{x}<\pi\:\Rightarrow\:\mathrm{sin}\:\mathrm{2x}\:=? \\ $$
Answered by iloveisrael last updated on 22/Jul/21
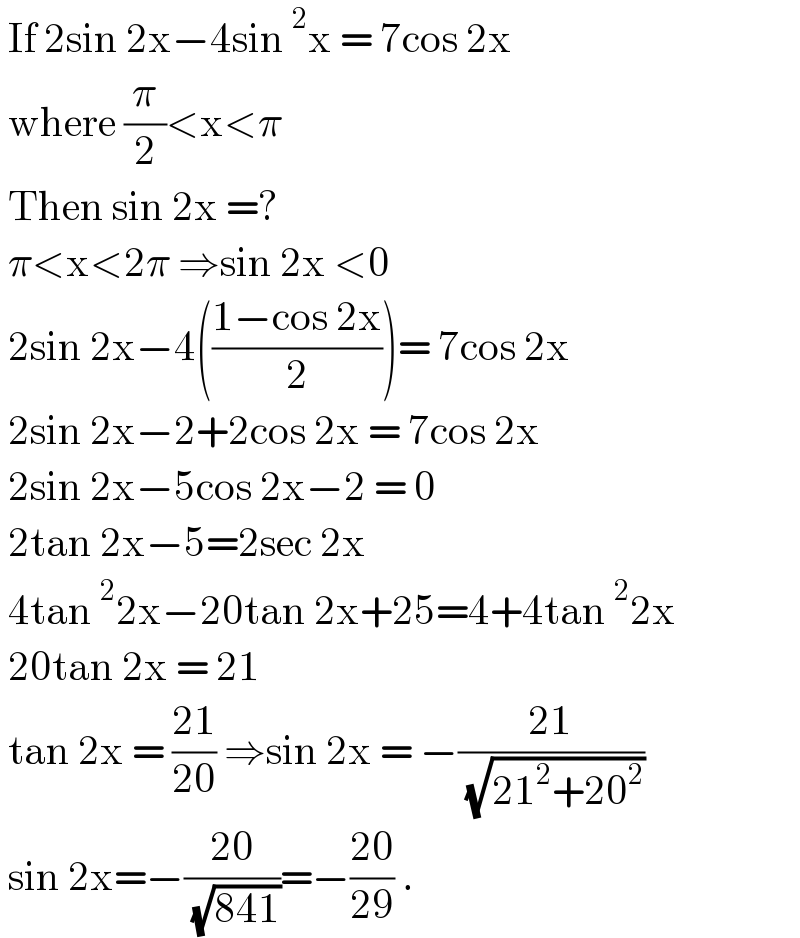
$$\:\mathrm{If}\:\mathrm{2sin}\:\mathrm{2x}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{7cos}\:\mathrm{2x}\: \\ $$ $$\:\mathrm{where}\:\frac{\pi}{\mathrm{2}}<\mathrm{x}<\pi \\ $$ $$\:\mathrm{Then}\:\mathrm{sin}\:\mathrm{2x}\:=?\: \\ $$ $$\:\pi<\mathrm{x}<\mathrm{2}\pi\:\Rightarrow\mathrm{sin}\:\mathrm{2x}\:<\mathrm{0} \\ $$ $$\:\mathrm{2sin}\:\mathrm{2x}−\mathrm{4}\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}}\right)=\:\mathrm{7cos}\:\mathrm{2x} \\ $$ $$\:\mathrm{2sin}\:\mathrm{2x}−\mathrm{2}+\mathrm{2cos}\:\mathrm{2x}\:=\:\mathrm{7cos}\:\mathrm{2x} \\ $$ $$\:\mathrm{2sin}\:\mathrm{2x}−\mathrm{5cos}\:\mathrm{2x}−\mathrm{2}\:=\:\mathrm{0} \\ $$ $$\:\mathrm{2tan}\:\mathrm{2x}−\mathrm{5}=\mathrm{2sec}\:\mathrm{2x} \\ $$ $$\:\mathrm{4tan}\:^{\mathrm{2}} \mathrm{2x}−\mathrm{20tan}\:\mathrm{2x}+\mathrm{25}=\mathrm{4}+\mathrm{4tan}\:^{\mathrm{2}} \mathrm{2x} \\ $$ $$\:\mathrm{20tan}\:\mathrm{2x}\:=\:\mathrm{21} \\ $$ $$\:\mathrm{tan}\:\mathrm{2x}\:=\:\frac{\mathrm{21}}{\mathrm{20}}\:\Rightarrow\mathrm{sin}\:\mathrm{2x}\:=\:−\frac{\mathrm{21}}{\:\sqrt{\mathrm{21}^{\mathrm{2}} +\mathrm{20}^{\mathrm{2}} }} \\ $$ $$\:\mathrm{sin}\:\mathrm{2x}=−\frac{\mathrm{20}}{\:\sqrt{\mathrm{841}}}=−\frac{\mathrm{20}}{\mathrm{29}}\:. \\ $$
