
Question Number 147569 by Sozan last updated on 21/Jul/21
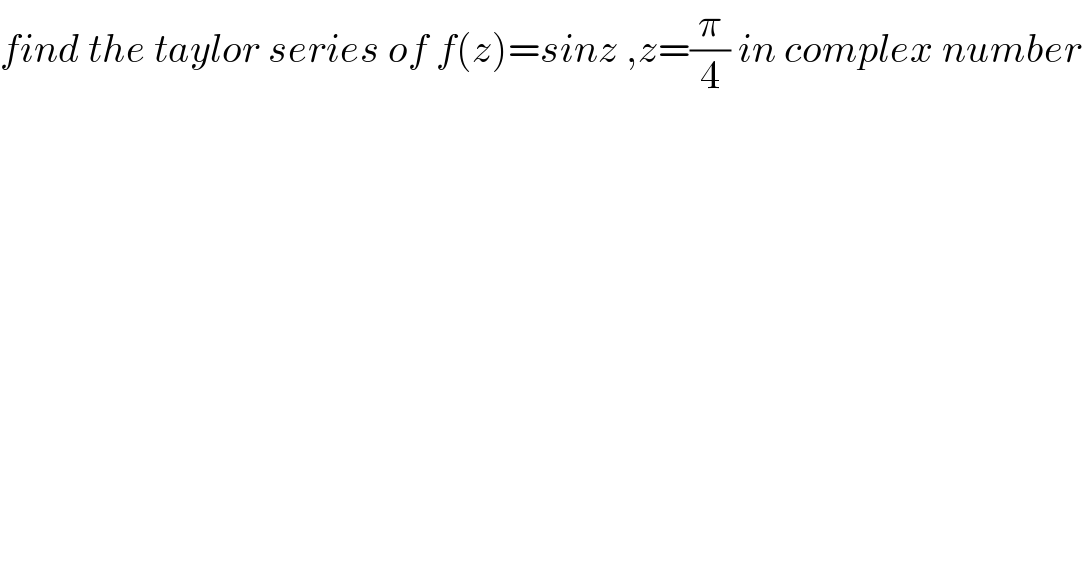
$${find}\:{the}\:{taylor}\:{series}\:{of}\:{f}\left({z}\right)={sinz}\:,{z}=\frac{\pi}{\mathrm{4}}\:{in}\:{complex}\:{number} \\ $$
Answered by mathmax by abdo last updated on 22/Jul/21
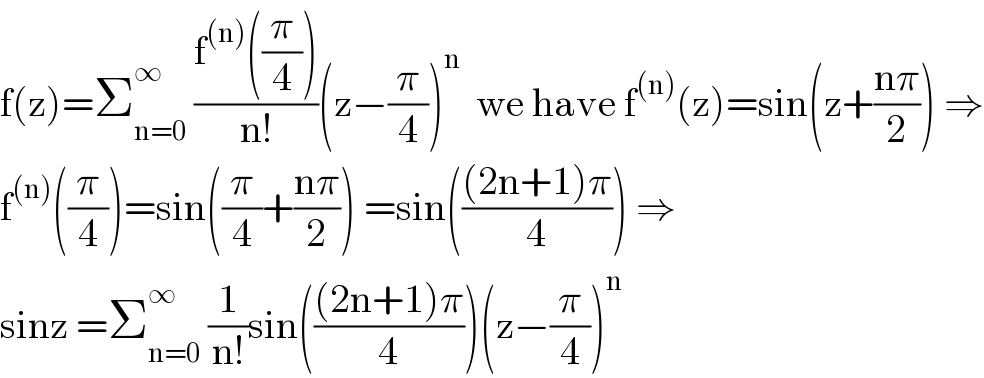
$$\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\frac{\pi}{\mathrm{4}}\right)}{\mathrm{n}!}\left(\mathrm{z}−\frac{\pi}{\mathrm{4}}\right)^{\mathrm{n}} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{z}\right)=\mathrm{sin}\left(\mathrm{z}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\:=\mathrm{sin}\left(\frac{\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$$\mathrm{sinz}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}!}\mathrm{sin}\left(\frac{\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{4}}\right)\left(\mathrm{z}−\frac{\pi}{\mathrm{4}}\right)^{\mathrm{n}} \\ $$
