
Question Number 147187 by mathdanisur last updated on 18/Jul/21
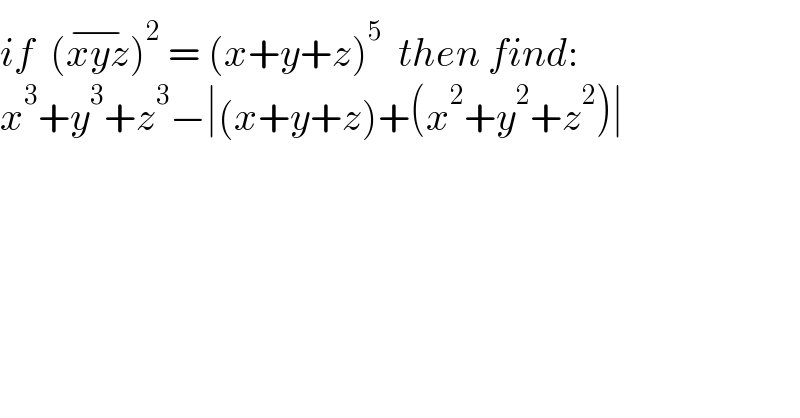
$${if}\:\:\left(\overline {{xyz}}\right)^{\mathrm{2}} \:=\:\left({x}+{y}+{z}\right)^{\mathrm{5}} \:\:{then}\:{find}: \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mid\left({x}+{y}+{z}\right)+\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)\mid \\ $$
Commented by Rasheed.Sindhi last updated on 18/Jul/21

$${Is}\:\overline {{xyz}}\:{a}\:{digital}\:{representation}\:{of} \\ $$$${decimal}\:{number}? \\ $$
Commented by mathdanisur last updated on 18/Jul/21

$${Yes}\:{Ser} \\ $$
Answered by Rasheed.Sindhi last updated on 19/Jul/21
![( xyz ^(−) )^2 =(x+y+z)^5 ▶ xyz ^(−) is 3-digit natural number ▶ ( xyz ^(−) )^2 is perfect 5th power ⇒ xyz ^(−) is perfect 5th power The only three digit number which is also 5th power is 243(=3^5 ) [ 2^5 =32 2-digit number × 3^5 =243 3-digit number✓ 4^5 =1024 4-digit number× ] Possible candidate is only 243 and it also fulfills the given condition : (243)^2 =^(?) (2+4+3)^5 (3^5 )^2 =^(?) 9^5 (3^5 )^2 =^(?) (3^2 )^5 3^(10) =3^(10) ∴ 243 is only successful candidate. ∴ x=2,y=4,z=3 x^3 +y^3 +z^3 −∣(x+y+z)+(x^2 +y^2 +z^2 )∣ =2^3 +4^3 +3^3 −∣(2+4+3)+(2^2 +3^2 +4^2 ∣ =8+64+27−∣9+29∣ =61](Q147220.png)
$$\:\left(\overline {\:{xyz}\:}\right)^{\mathrm{2}} =\left({x}+{y}+{z}\right)^{\mathrm{5}} \\ $$$$\blacktriangleright\:\overline {\:{xyz}\:}\:{is}\:\mathrm{3}-{digit}\:{natural}\:{number} \\ $$$$\blacktriangleright\:\:\left(\overline {\:{xyz}\:}\right)^{\mathrm{2}} \:{is}\:{perfect}\:\mathrm{5}{th}\:{power}\: \\ $$$$\:\:\:\:\:\:\Rightarrow\overline {\:{xyz}\:}\:{is}\:{perfect}\:\:\mathrm{5}{th}\:{power} \\ $$$${The}\:{only}\:{three}\:{digit}\:{number}\:{which} \\ $$$${is}\:{also}\:\mathrm{5}{th}\:{power}\:{is}\:\mathrm{243}\left(=\mathrm{3}^{\mathrm{5}} \right) \\ $$$$\:\:\:\left[\:\:\mathrm{2}^{\mathrm{5}} =\mathrm{32}\:\:\mathrm{2}-{digit}\:{number}\:×\right. \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{5}} =\mathrm{243}\:\:\mathrm{3}-{digit}\:{number}\checkmark \\ $$$$\left.\:\:\:\:\:\:\:\:\:\mathrm{4}^{\mathrm{5}} =\mathrm{1024}\:\:\mathrm{4}-{digit}\:{number}×\:\:\:\right] \\ $$$${Possible}\:{candidate}\:{is}\:{only}\:\mathrm{243}\:{and} \\ $$$${it}\:{also}\:{fulfills}\:{the}\:{given}\:{condition}\:: \\ $$$$\:\:\:\left(\mathrm{243}\right)^{\mathrm{2}} \overset{?} {=}\left(\mathrm{2}+\mathrm{4}+\mathrm{3}\right)^{\mathrm{5}} \\ $$$$\:\:\:\:\:\left(\mathrm{3}^{\mathrm{5}} \right)^{\mathrm{2}} \overset{?} {=}\mathrm{9}^{\mathrm{5}} \\ $$$$\:\:\:\:\left(\mathrm{3}^{\mathrm{5}} \right)^{\mathrm{2}} \:\overset{?} {=}\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\mathrm{3}^{\mathrm{10}} =\mathrm{3}^{\mathrm{10}} \\ $$$$\therefore\:\mathrm{243}\:{is}\:{only}\:{successful}\:{candidate}. \\ $$$$\therefore\:{x}=\mathrm{2},{y}=\mathrm{4},{z}=\mathrm{3} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mid\left({x}+{y}+{z}\right)+\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)\mid \\ $$$$=\mathrm{2}^{\mathrm{3}} +\mathrm{4}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} −\mid\left(\mathrm{2}+\mathrm{4}+\mathrm{3}\right)+\left(\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \mid\right. \\ $$$$=\mathrm{8}+\mathrm{64}+\mathrm{27}−\mid\mathrm{9}+\mathrm{29}\mid \\ $$$$=\mathrm{61} \\ $$
Commented by mathdanisur last updated on 19/Jul/21

$${cool}\:{Ser}\:{thanks} \\ $$
