
Question Number 147149 by nadovic last updated on 18/Jul/21

$$\:\mathrm{Two}\:\mathrm{concurrent}\:\mathrm{forces}\:\boldsymbol{{F}}_{\mathrm{1}} \:=\:\mathrm{12N}\:\mathrm{and} \\ $$$$\:\boldsymbol{{F}}_{\mathrm{2}} \:=\:\mathrm{30N}\:\mathrm{are}\:\mathrm{150}°\:\mathrm{apart}.\:\mathrm{Calculate}\: \\ $$$$\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between}\:\boldsymbol{{F}}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{the}\:\mathrm{resultant} \\ $$$$\:\mathrm{force}. \\ $$
Answered by Olaf_Thorendsen last updated on 18/Jul/21
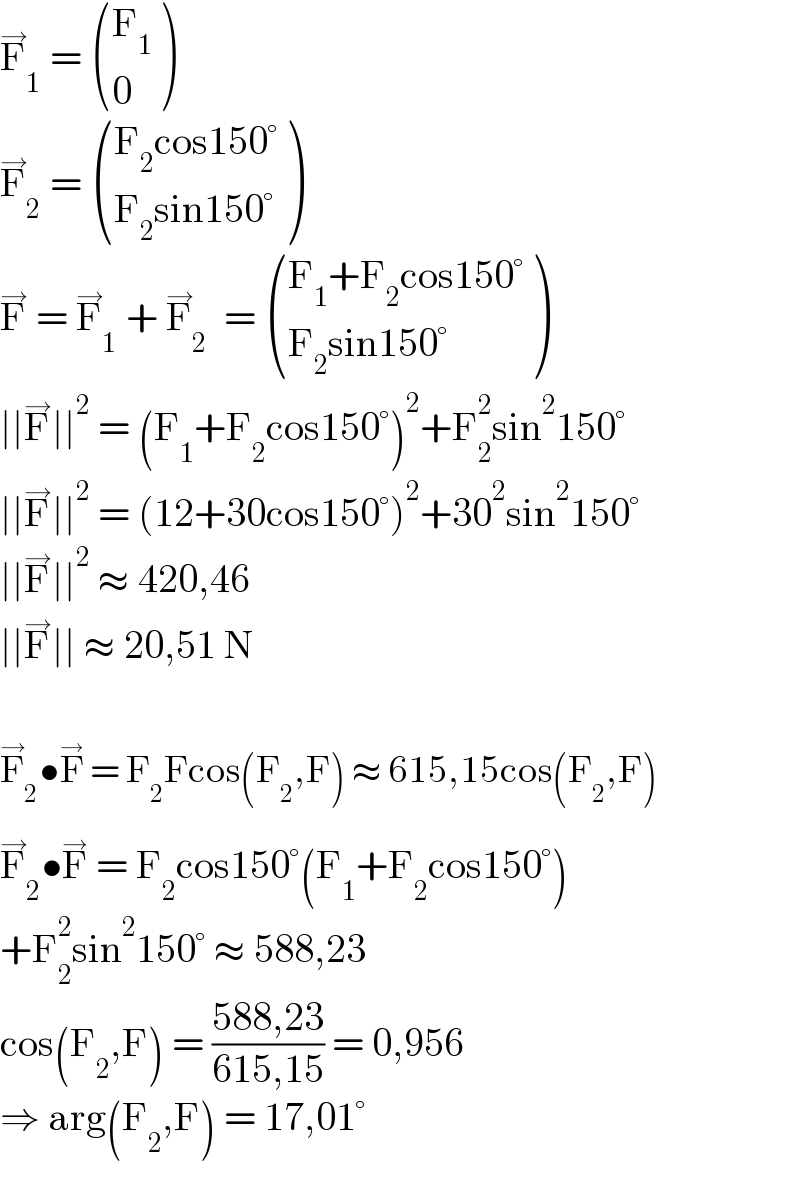
$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{1}} \:=\:\begin{pmatrix}{\mathrm{F}_{\mathrm{1}} }\\{\mathrm{0}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{F}_{\mathrm{2}} \mathrm{cos150}°}\\{\mathrm{F}_{\mathrm{2}} \mathrm{sin150}°}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{F}}\:=\:\overset{\rightarrow} {\mathrm{F}}_{\mathrm{1}} \:+\:\overset{\rightarrow} {\mathrm{F}}_{\mathrm{2}} \:\:=\:\begin{pmatrix}{\mathrm{F}_{\mathrm{1}} +\mathrm{F}_{\mathrm{2}} \mathrm{cos150}°}\\{\mathrm{F}_{\mathrm{2}} \mathrm{sin150}°}\end{pmatrix} \\ $$$$\mid\mid\overset{\rightarrow} {\mathrm{F}}\mid\mid^{\mathrm{2}} \:=\:\left(\mathrm{F}_{\mathrm{1}} +\mathrm{F}_{\mathrm{2}} \mathrm{cos150}°\right)^{\mathrm{2}} +\mathrm{F}_{\mathrm{2}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{150}° \\ $$$$\mid\mid\overset{\rightarrow} {\mathrm{F}}\mid\mid^{\mathrm{2}} \:=\:\left(\mathrm{12}+\mathrm{30cos150}°\right)^{\mathrm{2}} +\mathrm{30}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{150}° \\ $$$$\mid\mid\overset{\rightarrow} {\mathrm{F}}\mid\mid^{\mathrm{2}} \:\approx\:\mathrm{420},\mathrm{46} \\ $$$$\mid\mid\overset{\rightarrow} {\mathrm{F}}\mid\mid\:\approx\:\mathrm{20},\mathrm{51}\:\mathrm{N} \\ $$$$ \\ $$$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{2}} \bullet\overset{\rightarrow} {\mathrm{F}}\:=\:\mathrm{F}_{\mathrm{2}} \mathrm{Fcos}\left(\mathrm{F}_{\mathrm{2}} ,\mathrm{F}\right)\:\approx\:\mathrm{615},\mathrm{15cos}\left(\mathrm{F}_{\mathrm{2}} ,\mathrm{F}\right) \\ $$$$\overset{\rightarrow} {\mathrm{F}}_{\mathrm{2}} \bullet\overset{\rightarrow} {\mathrm{F}}\:=\:\mathrm{F}_{\mathrm{2}} \mathrm{cos150}°\left(\mathrm{F}_{\mathrm{1}} +\mathrm{F}_{\mathrm{2}} \mathrm{cos150}°\right) \\ $$$$+\mathrm{F}_{\mathrm{2}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{150}°\:\approx\:\mathrm{588},\mathrm{23} \\ $$$$\mathrm{cos}\left(\mathrm{F}_{\mathrm{2}} ,\mathrm{F}\right)\:=\:\frac{\mathrm{588},\mathrm{23}}{\mathrm{615},\mathrm{15}}\:=\:\mathrm{0},\mathrm{956} \\ $$$$\Rightarrow\:\mathrm{arg}\left(\mathrm{F}_{\mathrm{2}} ,\mathrm{F}\right)\:=\:\mathrm{17},\mathrm{01}° \\ $$
Commented by nadovic last updated on 18/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$
