
Question Number 147144 by gsk2684 last updated on 18/Jul/21

$${prove}\:{that}\: \\ $$$${equation}\:{of}\:{a}\:{circle}\:{passing}\:{through} \\ $$$${the}\:{points}\:{of}\:{intersection}\:{of}\:{a}\:{circle} \\ $$$${S}=\mathrm{0}\:{and}\:{a}\:{line}\:{L}=\mathrm{0}\:{can}\:{be}\:{taken}\:{as} \\ $$$${S}+\lambda{L}=\mathrm{0}\:{where}\:\lambda\:{is}\:{a}\:{parameter} \\ $$
Answered by mr W last updated on 18/Jul/21
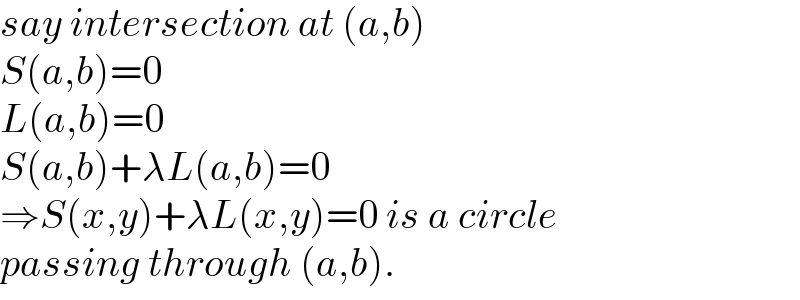
$${say}\:{intersection}\:{at}\:\left({a},{b}\right) \\ $$$${S}\left({a},{b}\right)=\mathrm{0} \\ $$$${L}\left({a},{b}\right)=\mathrm{0} \\ $$$${S}\left({a},{b}\right)+\lambda{L}\left({a},{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{S}\left({x},{y}\right)+\lambda{L}\left({x},{y}\right)=\mathrm{0}\:{is}\:{a}\:{circle} \\ $$$${passing}\:{through}\:\left({a},{b}\right). \\ $$
Commented by gsk2684 last updated on 20/Jul/21

$${ofcourse}\:{when}\:{two}\:{curves}\:{intersect}\: \\ $$$${at}\:{a}\:{point}\:{P}\:\:{then}\:{it}\:{satifies}\:{both}\: \\ $$$${the}\:{equation}.\: \\ $$$${i}\:{need}\:{to}\:{know}\:{how}\:{can}\:{we}\:{prove}\: \\ $$$${that}\:{general}\:{form}\:{represent}\:{a}\:{circle}? \\ $$
Commented by mr W last updated on 20/Jul/21
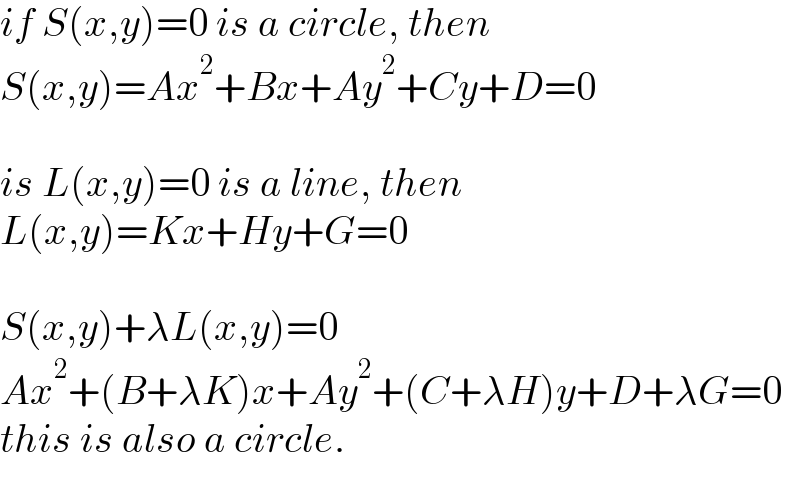
$${if}\:{S}\left({x},{y}\right)=\mathrm{0}\:{is}\:{a}\:{circle},\:{then} \\ $$$${S}\left({x},{y}\right)={Ax}^{\mathrm{2}} +{Bx}+{Ay}^{\mathrm{2}} +{Cy}+{D}=\mathrm{0} \\ $$$$ \\ $$$${is}\:{L}\left({x},{y}\right)=\mathrm{0}\:{is}\:{a}\:{line},\:{then} \\ $$$${L}\left({x},{y}\right)={Kx}+{Hy}+{G}=\mathrm{0} \\ $$$$ \\ $$$${S}\left({x},{y}\right)+\lambda{L}\left({x},{y}\right)=\mathrm{0} \\ $$$${Ax}^{\mathrm{2}} +\left({B}+\lambda{K}\right){x}+{Ay}^{\mathrm{2}} +\left({C}+\lambda{H}\right){y}+{D}+\lambda{G}=\mathrm{0} \\ $$$${this}\:{is}\:{also}\:{a}\:{circle}. \\ $$
Commented by gsk2684 last updated on 21/Jul/21
![condition that the equation ax^2 +ay^2 +2gx+2fy+c=0 represent a circle is g^2 +f^2 −ac ≥ 0 ∵radius ≥0 i would like to verify the condition (((B+λK)/2))^2 +(((C+λH)/2))^2 −A(D+λG) ≥0 consider (((B+λK)/2))^2 +(((C+λH)/2))^2 −A(D+λG) [((B/2))^2 +((C/2))^2 −AD]+λ(BK+CH−AG)+((λ^2 (K^2 +H^2 ))/4) some confusion to proceed from this](Q147457.png)
$${condition}\:{that}\:{the}\:{equation}\: \\ $$$${ax}^{\mathrm{2}} +{ay}^{\mathrm{2}} +\mathrm{2}{gx}+\mathrm{2}{fy}+{c}=\mathrm{0}\:{represent} \\ $$$${a}\:{circle}\:{is}\:{g}^{\mathrm{2}} +{f}^{\mathrm{2}} −{ac}\:\geqslant\:\mathrm{0}\:\because{radius}\:\geqslant\mathrm{0} \\ $$$${i}\:{would}\:{like}\:{to}\:{verify}\:{the}\:{condition}\: \\ $$$$\left(\frac{{B}+\lambda{K}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{C}+\lambda{H}}{\mathrm{2}}\right)^{\mathrm{2}} −{A}\left({D}+\lambda{G}\right)\:\geqslant\mathrm{0} \\ $$$${consider}\: \\ $$$$\left(\frac{{B}+\lambda{K}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{C}+\lambda{H}}{\mathrm{2}}\right)^{\mathrm{2}} −{A}\left({D}+\lambda{G}\right) \\ $$$$\left[\left(\frac{{B}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{C}}{\mathrm{2}}\right)^{\mathrm{2}} −{AD}\right]+\lambda\left({BK}+{CH}−{AG}\right)+\frac{\lambda^{\mathrm{2}} \left({K}^{\mathrm{2}} +{H}^{\mathrm{2}} \right)}{\mathrm{4}} \\ $$$${some}\:{confusion}\:{to}\:{proceed}\:{from}\:{this}\: \\ $$
