
Question Number 146669 by Ar Brandon last updated on 14/Jul/21
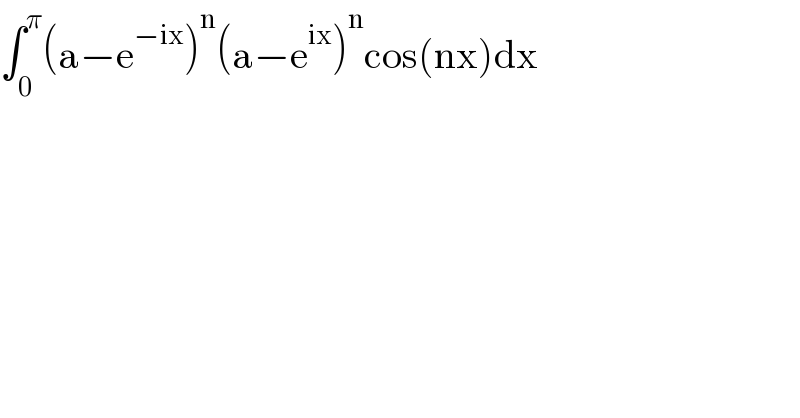
$$\int_{\mathrm{0}} ^{\pi} \left(\mathrm{a}−\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{n}} \left(\mathrm{a}−\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{n}} \mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx} \\ $$
Answered by mindispower last updated on 14/Jul/21

$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left({a}−{e}^{−{ix}} \right)\left({a}−{e}^{{ix}} \right)^{{n}} {cos}\left({nx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \left({a}−{e}^{−{ix}} \right)^{{n}} \left({a}−{e}^{{ix}} \right)^{{n}} {cos}\left({nx}\right){dx}+ \\ $$$$\int_{\pi} ^{\mathrm{2}\pi} \left({a}−{e}^{−{ix}} \right)^{{n}} \left({a}−{e}^{{ix}} \right)^{{n}} {cos}\left({nx}\right){dx} \\ $$$$={A}+{B},{B},{x}\rightarrow\mathrm{2}\pi−{x} \\ $$$${B}\Leftrightarrow\int_{\mathrm{0}} ^{\pi} \left({a}−{e}^{{ix}} \right)^{{n}} \left({a}−{e}^{−{ix}} \right)^{{n}} {cos}\left({nx}\right)={A} \\ $$$$\mathrm{2}{A}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left({a}−\frac{\mathrm{1}}{{e}^{{ix}} }\right)^{{n}} \left({a}−{e}^{{ix}} \right)^{{n}} .\frac{{e}^{{inx}} −{e}^{−{inx}} }{\mathrm{2}}. \\ $$$${e}^{{ix}} ={z} \\ $$$$\Rightarrow\int_{{C}} \frac{\left({az}−\mathrm{1}\right)^{{n}} \left({a}−{z}\right)^{{n}} }{{z}^{{n}} }.\frac{{z}^{\mathrm{2}{n}} −\mathrm{1}}{\mathrm{2}{z}^{{n}} }.\frac{\mathrm{1}}{{iz}}{dz}=\mathrm{2}{i}\pi\:{Res}\left({f},\mathrm{0}\right) \\ $$$$=\int_{{C}} \frac{\left({az}−\mathrm{1}\right)^{{n}} \left({a}−{z}\right)^{{n}} }{\mathrm{2}{iz}}−\frac{\mathrm{1}}{\mathrm{2}{iz}^{\mathrm{2}{n}+\mathrm{1}} }\left({az}−\mathrm{1}\right)\left({a}−{z}\right){dz} \\ $$$$=\pi\left(−\mathrm{1}\right)^{{n}} {a}^{{n}} −\pi\left(−\mathrm{1}\right)^{{n}} {a}^{{n}} =\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 15/Jul/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
