
Question Number 145451 by math55 last updated on 05/Jul/21
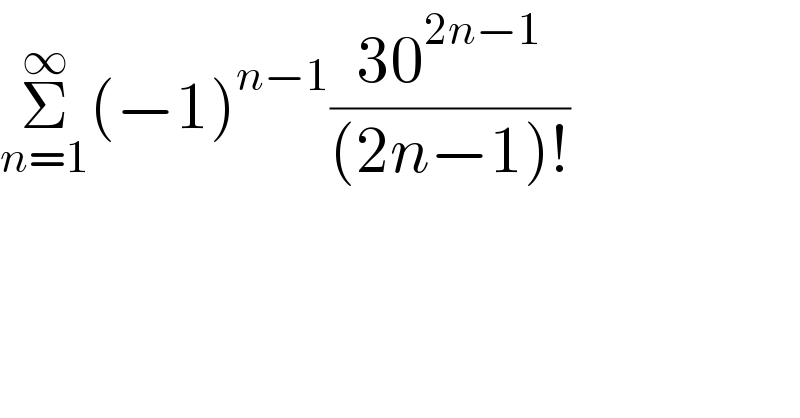
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{\mathrm{30}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$
Answered by Olaf_Thorendsen last updated on 05/Jul/21
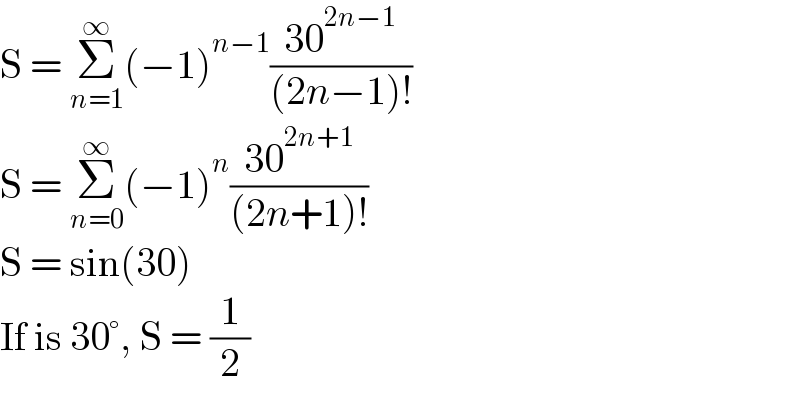
$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{\mathrm{30}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{30}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\mathrm{S}\:=\:\mathrm{sin}\left(\mathrm{30}\right) \\ $$$$\mathrm{If}\:\mathrm{is}\:\mathrm{30}°,\:\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by math55 last updated on 05/Jul/21
please sir is there anyway to prove that it's 1/2 without passing through sin30°
