
Question Number 144922 by mathdanisur last updated on 30/Jun/21
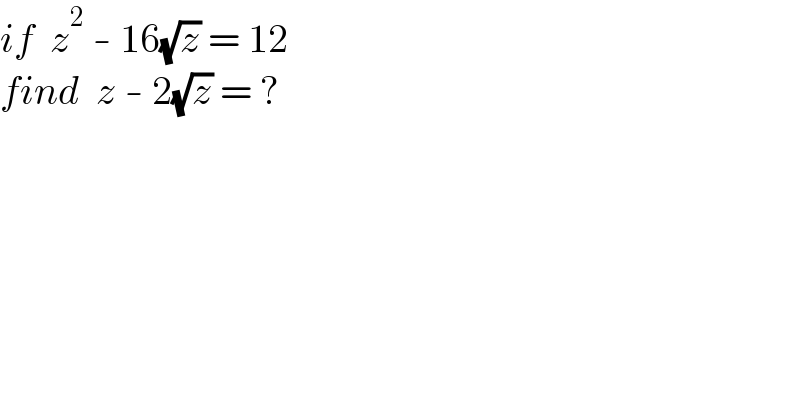
$${if}\:\:{z}^{\mathrm{2}} \:-\:\mathrm{16}\sqrt{{z}}\:=\:\mathrm{12} \\ $$$${find}\:\:{z}\:-\:\mathrm{2}\sqrt{{z}}\:=\:? \\ $$
Answered by liberty last updated on 30/Jun/21
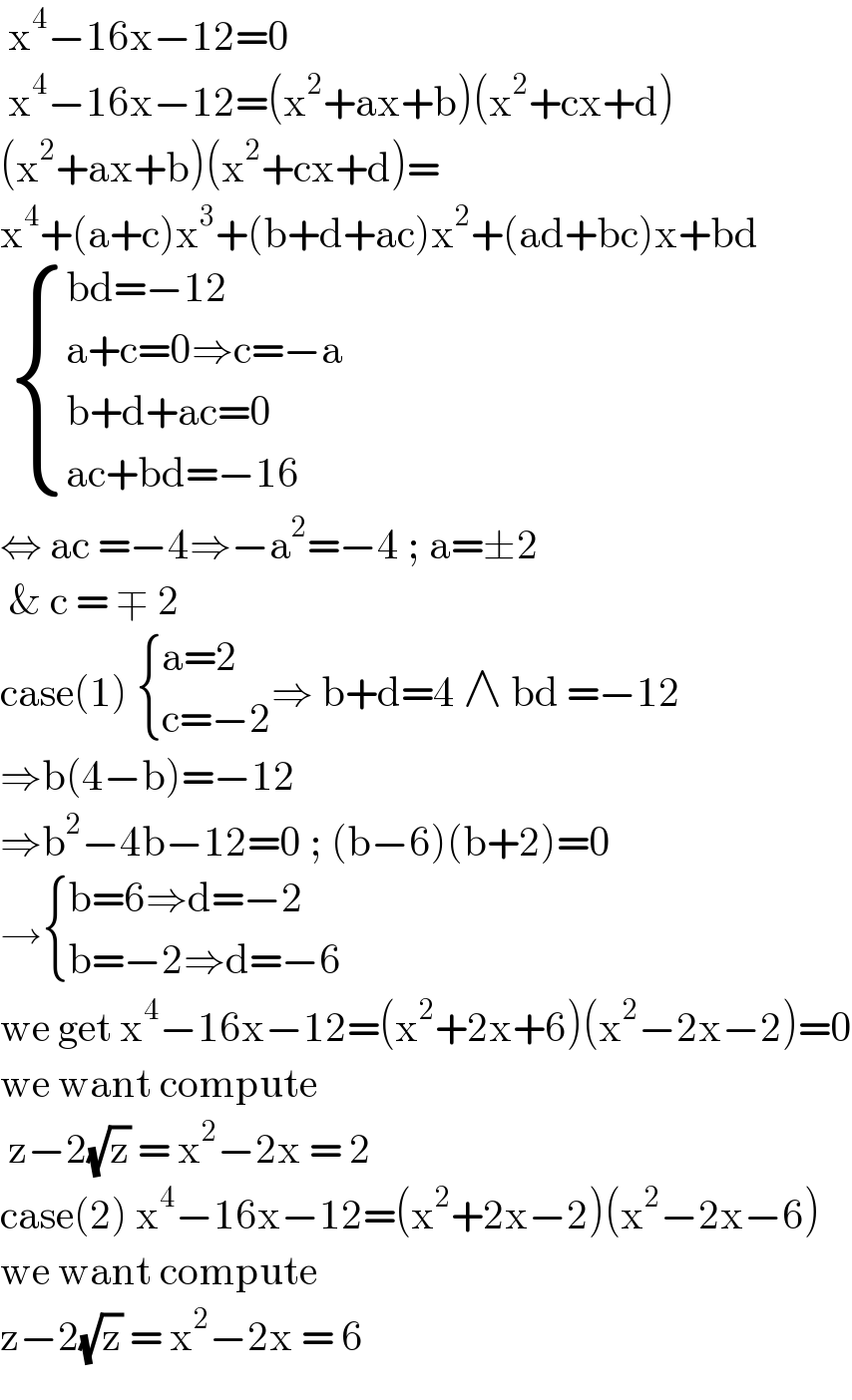
$$\:\mathrm{x}^{\mathrm{4}} −\mathrm{16x}−\mathrm{12}=\mathrm{0} \\ $$$$\:\mathrm{x}^{\mathrm{4}} −\mathrm{16x}−\mathrm{12}=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{cx}+\mathrm{d}\right) \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{cx}+\mathrm{d}\right)= \\ $$$$\mathrm{x}^{\mathrm{4}} +\left(\mathrm{a}+\mathrm{c}\right)\mathrm{x}^{\mathrm{3}} +\left(\mathrm{b}+\mathrm{d}+\mathrm{ac}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{ad}+\mathrm{bc}\right)\mathrm{x}+\mathrm{bd} \\ $$$$\:\begin{cases}{\mathrm{bd}=−\mathrm{12}}\\{\mathrm{a}+\mathrm{c}=\mathrm{0}\Rightarrow\mathrm{c}=−\mathrm{a}}\\{\mathrm{b}+\mathrm{d}+\mathrm{ac}=\mathrm{0}}\\{\mathrm{ac}+\mathrm{bd}=−\mathrm{16}}\end{cases} \\ $$$$\Leftrightarrow\:\mathrm{ac}\:=−\mathrm{4}\Rightarrow−\mathrm{a}^{\mathrm{2}} =−\mathrm{4}\:;\:\mathrm{a}=\pm\mathrm{2} \\ $$$$\:\&\:\mathrm{c}\:=\:\mp\:\mathrm{2}\: \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\begin{cases}{\mathrm{a}=\mathrm{2}}\\{\mathrm{c}=−\mathrm{2}}\end{cases}\Rightarrow\:\mathrm{b}+\mathrm{d}=\mathrm{4}\:\wedge\:\mathrm{bd}\:=−\mathrm{12} \\ $$$$\Rightarrow\mathrm{b}\left(\mathrm{4}−\mathrm{b}\right)=−\mathrm{12}\: \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} −\mathrm{4b}−\mathrm{12}=\mathrm{0}\:;\:\left(\mathrm{b}−\mathrm{6}\right)\left(\mathrm{b}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\rightarrow\begin{cases}{\mathrm{b}=\mathrm{6}\Rightarrow\mathrm{d}=−\mathrm{2}}\\{\mathrm{b}=−\mathrm{2}\Rightarrow\mathrm{d}=−\mathrm{6}}\end{cases} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{x}^{\mathrm{4}} −\mathrm{16x}−\mathrm{12}=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{want}\:\mathrm{compute}\: \\ $$$$\:\mathrm{z}−\mathrm{2}\sqrt{\mathrm{z}}\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\:=\:\mathrm{2} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{x}^{\mathrm{4}} −\mathrm{16x}−\mathrm{12}=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{6}\right) \\ $$$$\mathrm{we}\:\mathrm{want}\:\mathrm{compute}\: \\ $$$$\mathrm{z}−\mathrm{2}\sqrt{\mathrm{z}}\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\:=\:\mathrm{6}\: \\ $$
Commented by mathdanisur last updated on 30/Jun/21

$${thank}\:{you}\:{Sir} \\ $$
