
Question Number 144914 by bobhans last updated on 30/Jun/21
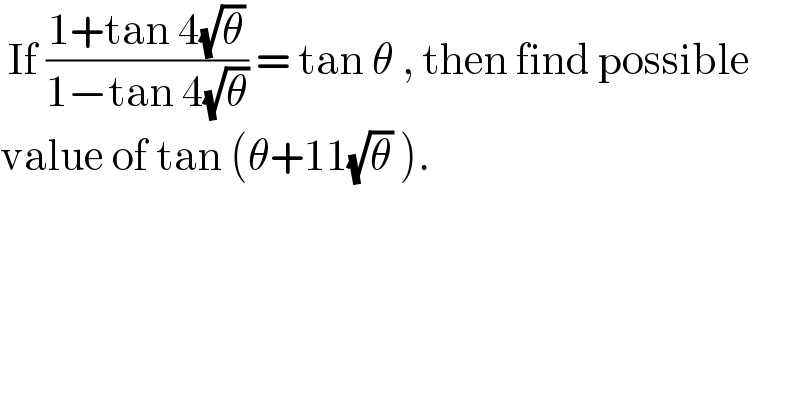
$$\:\mathrm{If}\:\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{4}\sqrt{\theta}}{\mathrm{1}−\mathrm{tan}\:\mathrm{4}\sqrt{\theta}}\:=\:\mathrm{tan}\:\theta\:,\:\mathrm{then}\:\mathrm{find}\:\mathrm{possible} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:\left(\theta+\mathrm{11}\sqrt{\theta}\:\right). \\ $$
Answered by imjagoll last updated on 30/Jun/21
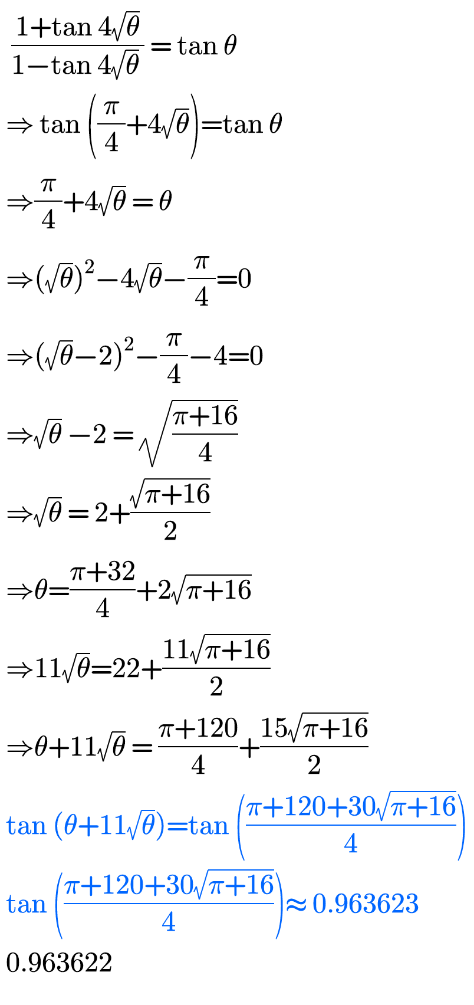
Answered by mr W last updated on 30/Jun/21

$$\:\frac{\mathrm{tan}\:\frac{\pi}{\mathrm{4}}+\mathrm{tan}\:\mathrm{4}\sqrt{\theta}}{\mathrm{1}−\mathrm{tan}\:\frac{\pi}{\mathrm{4}}×\mathrm{tan}\:\mathrm{4}\sqrt{\theta}}\:=\:\mathrm{tan}\:\theta \\ $$$$\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\mathrm{4}\sqrt{\theta}\right)\:=\:\mathrm{tan}\:\theta \\ $$$$\:{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{4}\sqrt{\theta}\:=\:\theta \\ $$$$\:{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{4}=\left(\sqrt{\theta}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\sqrt{\theta}=\mathrm{2}+\sqrt{{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{4}} \\ $$$$\Rightarrow{k}\geqslant−\mathrm{1} \\ $$$$\sqrt{\theta}=\mathrm{2}−\sqrt{{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{4}} \\ $$$$\Rightarrow{k}=−\mathrm{1} \\ $$$$ \\ $$$$\theta+\mathrm{11}\sqrt{\theta}=\:{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{15}\sqrt{\theta} \\ $$$$\theta+\mathrm{11}\sqrt{\theta}=\:{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{30}\pm\mathrm{15}\sqrt{{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{4}} \\ $$$$\Rightarrow\mathrm{tan}\:\left(\theta+\mathrm{11}\sqrt{\theta}\right)=\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\mathrm{30}+\mathrm{15}\sqrt{{k}\pi+\frac{\pi}{\mathrm{4}}+\mathrm{4}}\right)\:{with}\:{k}\geqslant−\mathrm{1} \\ $$$${or}\: \\ $$$$\Rightarrow\mathrm{tan}\:\left(\theta+\mathrm{11}\sqrt{\theta}\right)=\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\mathrm{30}−\mathrm{15}\sqrt{−\pi+\frac{\pi}{\mathrm{4}}+\mathrm{4}}\right) \\ $$
