
Question Number 143698 by Dwaipayan Shikari last updated on 17/Jun/21

$$\:{My}\:{first}\:{Contribution}\:{to}\:{this}\:{forum}.\: \\ $$$${One}\:{year}\:{later}\: \\ $$$${Q}\:\mathrm{98831} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Jun/21

$${Mad}\:{Question}\:{on}\:{that}\:{same}\:{day}.\:{Mr}.{MJS}\:{said}\:{that}\:{it} \\ $$$${Consists}\:{Hypergeometric}\:{function}\:.{I}\:{didn}'{t}\:{know} \\ $$$${About}\:{Hypergeometric}\:{functions} \\ $$$${Q}\mathrm{98951} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Jun/21
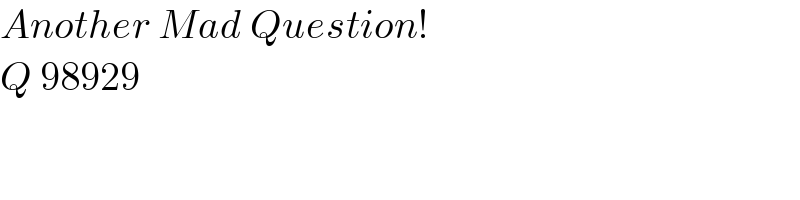
$${Another}\:{Mad}\:{Question}! \\ $$$${Q}\:\mathrm{98929} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Jun/21
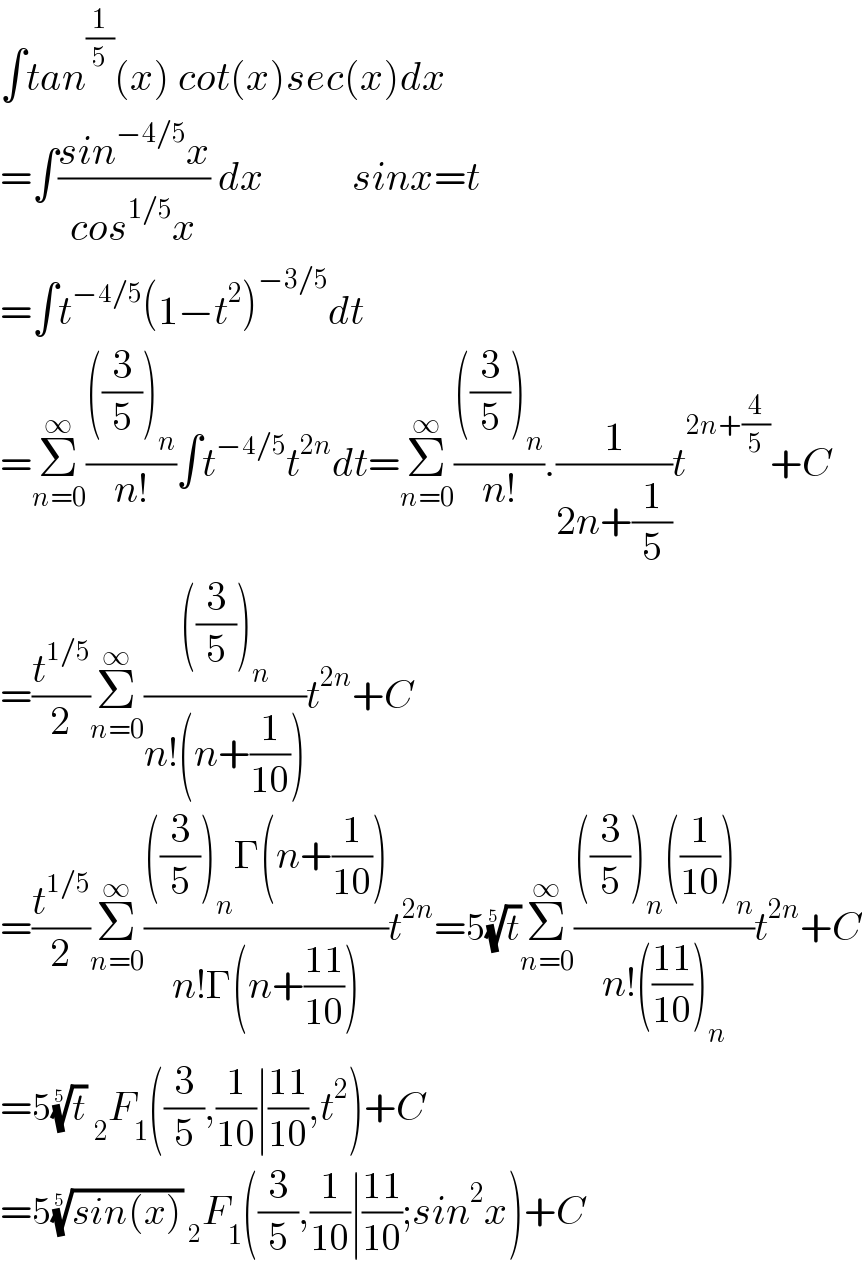
$$\int{tan}^{\frac{\mathrm{1}}{\mathrm{5}}} \left({x}\right)\:{cot}\left({x}\right){sec}\left({x}\right){dx} \\ $$$$=\int\frac{{sin}^{−\mathrm{4}/\mathrm{5}} {x}}{{cos}^{\mathrm{1}/\mathrm{5}} {x}}\:{dx}\:\:\:\:\:\:\:\:\:\:\:{sinx}={t} \\ $$$$=\int{t}^{−\mathrm{4}/\mathrm{5}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{−\mathrm{3}/\mathrm{5}} {dt}\:\:\: \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)_{{n}} }{{n}!}\int{t}^{−\mathrm{4}/\mathrm{5}} {t}^{\mathrm{2}{n}} {dt}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)_{{n}} }{{n}!}.\frac{\mathrm{1}}{\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{5}}}{t}^{\mathrm{2}{n}+\frac{\mathrm{4}}{\mathrm{5}}} +{C} \\ $$$$=\frac{{t}^{\mathrm{1}/\mathrm{5}} }{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)_{{n}} }{{n}!\left({n}+\frac{\mathrm{1}}{\mathrm{10}}\right)}{t}^{\mathrm{2}{n}} +{C} \\ $$$$=\frac{{t}^{\mathrm{1}/\mathrm{5}} }{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)_{{n}} \Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{10}}\right)}{{n}!\Gamma\left({n}+\frac{\mathrm{11}}{\mathrm{10}}\right)}{t}^{\mathrm{2}{n}} =\mathrm{5}\sqrt[{\mathrm{5}}]{{t}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)_{{n}} \left(\frac{\mathrm{1}}{\mathrm{10}}\right)_{{n}} }{{n}!\left(\frac{\mathrm{11}}{\mathrm{10}}\right)_{{n}} }{t}^{\mathrm{2}{n}} +{C} \\ $$$$=\mathrm{5}\sqrt[{\mathrm{5}}]{{t}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}},\frac{\mathrm{1}}{\mathrm{10}}\mid\frac{\mathrm{11}}{\mathrm{10}},{t}^{\mathrm{2}} \right)+{C} \\ $$$$=\mathrm{5}\sqrt[{\mathrm{5}}]{{sin}\left({x}\right)}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}},\frac{\mathrm{1}}{\mathrm{10}}\mid\frac{\mathrm{11}}{\mathrm{10}};{sin}^{\mathrm{2}} {x}\right)+{C} \\ $$
Commented by Ar Brandon last updated on 17/Jun/21
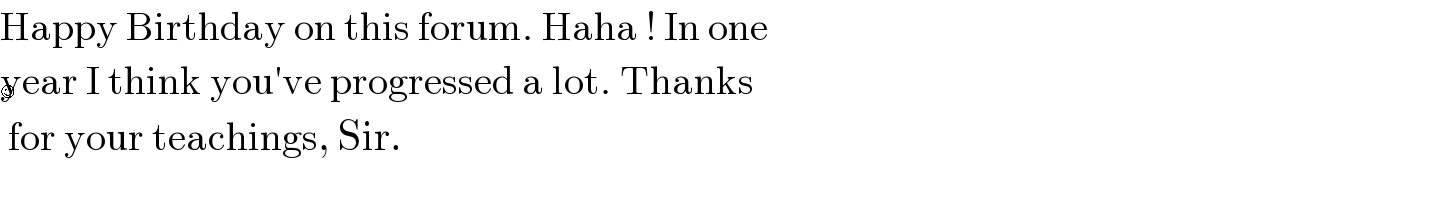
$$\mathrm{Happy}\:\mathrm{Birthday}\:\mathrm{on}\:\mathrm{this}\:\mathrm{forum}.\:\mathrm{Haha}\:!\:\mathrm{In}\:\mathrm{one}\: \\ $$$$\mathrm{year}\:\mathrm{I}\:\mathrm{think}\:\mathrm{you}'\mathrm{ve}\:\mathrm{progressed}\:\mathrm{a}\:\mathrm{lot}.\:\mathrm{Thanks} \\ $$$$\:\mathrm{for}\:\mathrm{your}\:\mathrm{teachings},\:\mathrm{Sir}. \\ $$😉
Commented by Dwaipayan Shikari last updated on 17/Jun/21
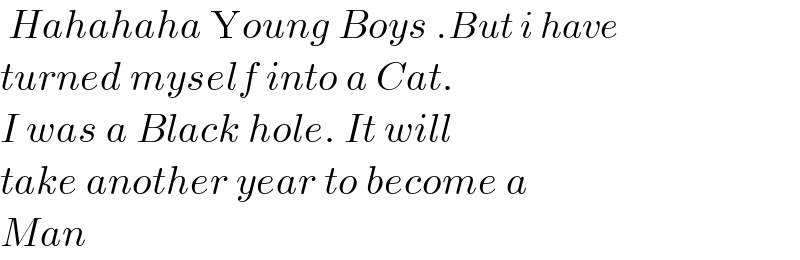
$$\:{Hahahaha}\:\mathrm{Y}{oung}\:{Boys}\:.{But}\:{i}\:{have}\: \\ $$$${turned}\:{myself}\:{into}\:{a}\:{Cat}. \\ $$$${I}\:{was}\:{a}\:{Black}\:{hole}.\:{It}\:{will} \\ $$$${take}\:{another}\:{year}\:{to}\:{become}\:{a}\: \\ $$$${Man} \\ $$
