
Question Number 143650 by Rankut last updated on 16/Jun/21
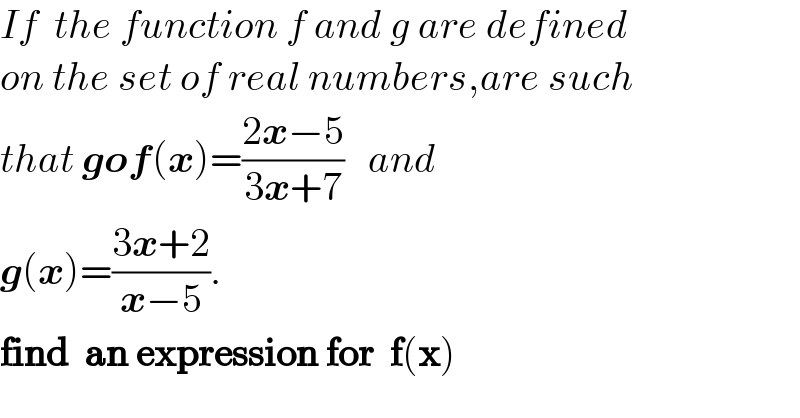
$${If}\:\:{the}\:{function}\:{f}\:{and}\:{g}\:{are}\:{defined} \\ $$$${on}\:{the}\:{set}\:{of}\:{real}\:{numbers},{are}\:{such} \\ $$$${that}\:\boldsymbol{{gof}}\left(\boldsymbol{{x}}\right)=\frac{\mathrm{2}\boldsymbol{{x}}−\mathrm{5}}{\mathrm{3}\boldsymbol{{x}}+\mathrm{7}}\:\:\:{and}\: \\ $$$$\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)=\frac{\mathrm{3}\boldsymbol{{x}}+\mathrm{2}}{\boldsymbol{{x}}−\mathrm{5}}. \\ $$$$\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{expression}}\:\boldsymbol{\mathrm{for}}\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$
Answered by ajfour last updated on 16/Jun/21
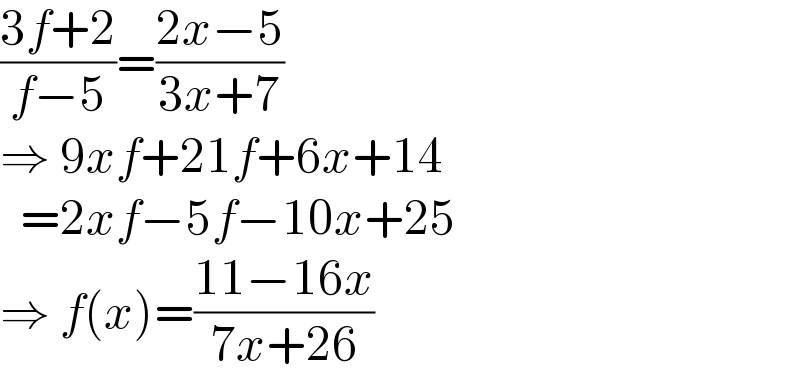
$$\frac{\mathrm{3}{f}+\mathrm{2}}{{f}−\mathrm{5}}=\frac{\mathrm{2}{x}−\mathrm{5}}{\mathrm{3}{x}+\mathrm{7}} \\ $$$$\Rightarrow\:\mathrm{9}{xf}+\mathrm{21}{f}+\mathrm{6}{x}+\mathrm{14} \\ $$$$\:\:=\mathrm{2}{xf}−\mathrm{5}{f}−\mathrm{10}{x}+\mathrm{25} \\ $$$$\Rightarrow\:{f}\left({x}\right)=\frac{\mathrm{11}−\mathrm{16}{x}}{\mathrm{7}{x}+\mathrm{26}} \\ $$
Answered by Olaf_Thorendsen last updated on 16/Jun/21
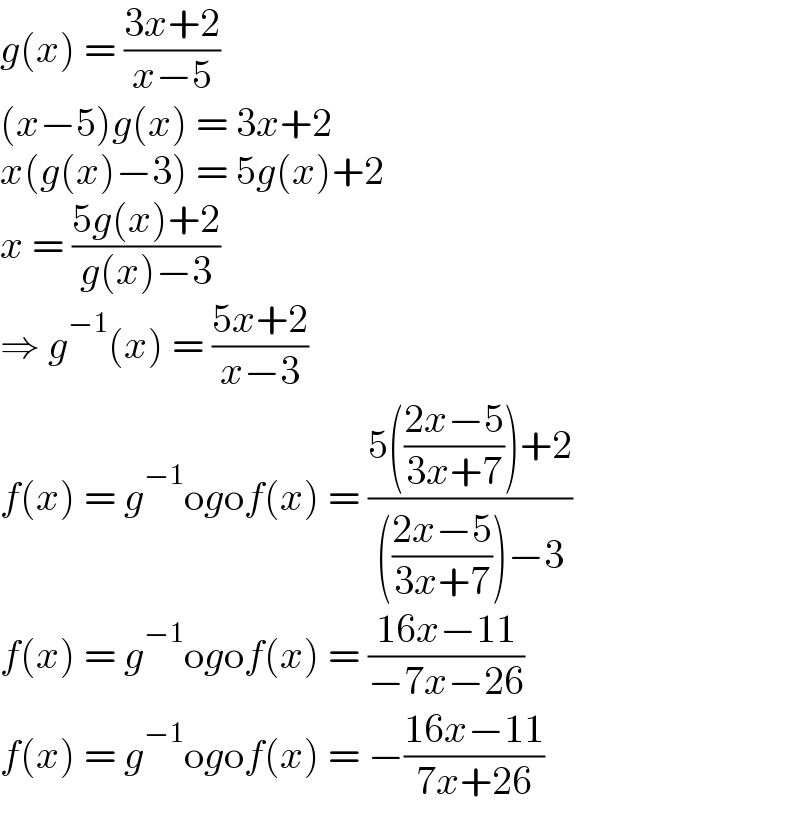
$${g}\left({x}\right)\:=\:\frac{\mathrm{3}{x}+\mathrm{2}}{{x}−\mathrm{5}} \\ $$$$\left({x}−\mathrm{5}\right){g}\left({x}\right)\:=\:\mathrm{3}{x}+\mathrm{2} \\ $$$${x}\left({g}\left({x}\right)−\mathrm{3}\right)\:=\:\mathrm{5}{g}\left({x}\right)+\mathrm{2} \\ $$$${x}\:=\:\frac{\mathrm{5}{g}\left({x}\right)+\mathrm{2}}{{g}\left({x}\right)−\mathrm{3}} \\ $$$$\Rightarrow\:{g}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{5}{x}+\mathrm{2}}{{x}−\mathrm{3}} \\ $$$${f}\left({x}\right)\:=\:{g}^{−\mathrm{1}} \mathrm{o}{g}\mathrm{o}{f}\left({x}\right)\:=\:\frac{\mathrm{5}\left(\frac{\mathrm{2}{x}−\mathrm{5}}{\mathrm{3}{x}+\mathrm{7}}\right)+\mathrm{2}}{\left(\frac{\mathrm{2}{x}−\mathrm{5}}{\mathrm{3}{x}+\mathrm{7}}\right)−\mathrm{3}} \\ $$$${f}\left({x}\right)\:=\:{g}^{−\mathrm{1}} \mathrm{o}{g}\mathrm{o}{f}\left({x}\right)\:=\:\frac{\mathrm{16}{x}−\mathrm{11}}{−\mathrm{7}{x}−\mathrm{26}} \\ $$$${f}\left({x}\right)\:=\:{g}^{−\mathrm{1}} \mathrm{o}{g}\mathrm{o}{f}\left({x}\right)\:=\:−\frac{\mathrm{16}{x}−\mathrm{11}}{\mathrm{7}{x}+\mathrm{26}} \\ $$
Answered by TheHoneyCat last updated on 16/Jun/21

$$ \\ $$$$\mathrm{let}\:{x}\in\mathbb{R} \\ $$$$\mathrm{and}\:{y}={f}\left({x}\right)\:_{\left(\mathrm{if}\:\mathrm{it}\:\mathrm{exists}\right)} \\ $$$$ \\ $$$$\left({x}−\mathrm{5}\right){g}\left({x}\right)=\mathrm{3}{x}+\mathrm{2} \\ $$$$\mathrm{so}\:\left({y}−\mathrm{5}\right){g}\left({y}\right)=\mathrm{3}{y}+\mathrm{2} \\ $$$$\mathrm{thus}\:\left({y}−\mathrm{5}\right)\left(\mathrm{2}{x}−\mathrm{5}\right)=\left(\mathrm{3}{y}+\mathrm{2}\right)\left(\mathrm{3}{x}+\mathrm{7}\right) \\ $$$$\Leftrightarrow\left(\mathrm{7}{x}+\mathrm{26}\right){y}=\mathrm{11}−\mathrm{16}{x} \\ $$$$ \\ $$$$\mathrm{so},\:{f}:\:\begin{cases}{\mathbb{R}\backslash\left\{\frac{−\mathrm{26}}{\mathrm{7}}\right\}}&{\rightarrow}&{\mathbb{R}}\\{{x}}&{\rightarrow}&{\frac{\mathrm{11}−\mathrm{16}{x}}{\mathrm{26}+\mathrm{7}{x}}}\end{cases} \\ $$$$ \\ $$$${I}\:{hope}\:{I}\:{did}\:{not}\:{make}\:{any}\:{calculation}\:{mistake} \\ $$$${but}\:{the}\:{reasonning}\:{is}\:{the}\:{right}\:{one}. \\ $$$$\left.;\bullet\right) \\ $$
