
Question Number 143638 by mnjuly1970 last updated on 16/Jun/21
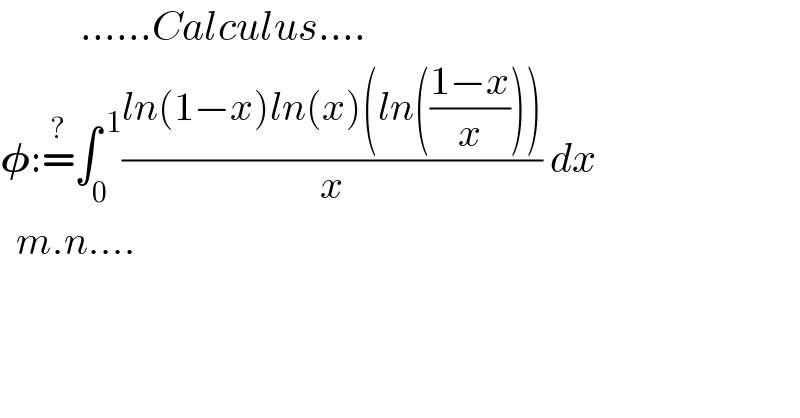
$$\:\:\:\:\:\:\:\:\:\:......{Calculus}.... \\ $$$$\boldsymbol{\phi}:\overset{?} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right){ln}\left({x}\right)\left({ln}\left(\frac{\mathrm{1}−{x}}{{x}}\right)\right)}{{x}}\:{dx} \\ $$$$\:\:{m}.{n}.... \\ $$$$ \\ $$
Commented by TheHoneyCat last updated on 17/Jun/21
![I did not get the result but here is the prof that it is well defined let α∈]0,1[ let f: x→((ln(1−x)lnx.ln((1/x)−1))/x) f∼_0 ((−x.lnx.ln((1/x)))/x) ∼_0 ln(x)^2 so ∫_0 ^α f is well defined if and only if ∫_0 ^α ln^2 is too (∗) ∫_0 ^α ln^2 =[(xlnx−x)lnx]_0 ^α −∫_0 ^α ((xlnx−x)/x)dx =(αlnα−α)lnα − 0 −∫_0 ^α (lnx − 1) dx =(αlnα−α)lnα +α −∫_0 ^α lnx dx =(αlnα−α)lnα +α −[xlnx−x]_0 ^α =(αlnα−α)(1+lnα) +α ∈R so ∫_0 ^α f∈R also: f∼_1 ((ln(1−x).x.ln(1−x))/1) ∼_1 ln(1−x)^2 considering y=x−1 it is obvious that we get the same integral as (∗) so ∫_α ^1 f∈R thus: ∫_0 ^1 f(x)dx ∈R](Q143674.png)
$$\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{get}\:\mathrm{the}\:\mathrm{result}\:\mathrm{but}\:\mathrm{here}\:\mathrm{is}\:\mathrm{the}\:\mathrm{prof}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{well}\:\mathrm{defined} \\ $$$$ \\ $$$$\left.\mathrm{let}\:\alpha\in\right]\mathrm{0},\mathrm{1}\left[\right. \\ $$$$\mathrm{let}\:\mathrm{f}:\:{x}\rightarrow\frac{\mathrm{ln}\left(\mathrm{1}−{x}\right)\mathrm{ln}{x}.\mathrm{ln}\left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}{{x}} \\ $$$${f}\underset{\mathrm{0}} {\sim}\frac{−{x}.\mathrm{ln}{x}.\mathrm{ln}\left(\frac{\mathrm{1}}{{x}}\right)}{{x}} \\ $$$$\underset{\mathrm{0}} {\sim}\mathrm{ln}\left({x}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{so}\:\int_{\mathrm{0}} ^{\alpha} {f}\:\:\:\mathrm{is}\:\mathrm{well}\:\mathrm{defined}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\int_{\mathrm{0}} ^{\alpha} \mathrm{ln}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{too}\:\:\left(\ast\right) \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\alpha} \mathrm{ln}^{\mathrm{2}} =\left[\left({x}\mathrm{ln}{x}−{x}\right)\mathrm{ln}{x}\right]_{\mathrm{0}} ^{\alpha} −\int_{\mathrm{0}} ^{\alpha} \frac{{x}\mathrm{ln}{x}−{x}}{{x}}{dx} \\ $$$$=\left(\alpha\mathrm{ln}\alpha−\alpha\right)\mathrm{ln}\alpha\:−\:\mathrm{0}\:−\int_{\mathrm{0}} ^{\alpha} \left(\mathrm{ln}{x}\:−\:\mathrm{1}\right)\:{dx} \\ $$$$=\left(\alpha\mathrm{ln}\alpha−\alpha\right)\mathrm{ln}\alpha\:+\alpha\:−\int_{\mathrm{0}} ^{\alpha} \mathrm{ln}{x}\:{dx} \\ $$$$=\left(\alpha\mathrm{ln}\alpha−\alpha\right)\mathrm{ln}\alpha\:+\alpha\:−\left[{x}\mathrm{ln}{x}−{x}\right]_{\mathrm{0}} ^{\alpha} \\ $$$$=\left(\alpha\mathrm{ln}\alpha−\alpha\right)\left(\mathrm{1}+\mathrm{ln}\alpha\right)\:+\alpha\:\in\mathbb{R} \\ $$$$\mathrm{so}\:\int_{\mathrm{0}} ^{\alpha} {f}\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{also}: \\ $$$${f}\underset{\mathrm{1}} {\sim}\frac{\mathrm{ln}\left(\mathrm{1}−{x}\right).{x}.\mathrm{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}} \\ $$$$\underset{\mathrm{1}} {\sim}\mathrm{ln}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{considering}\:{y}={x}−\mathrm{1} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{obvious}\:\mathrm{that}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{integral}\:\mathrm{as}\:\left(\ast\right) \\ $$$$\mathrm{so}\:\int_{\alpha} ^{\mathrm{1}} {f}\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{thus}: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:\in\mathbb{R} \\ $$
Commented by mnjuly1970 last updated on 17/Jun/21
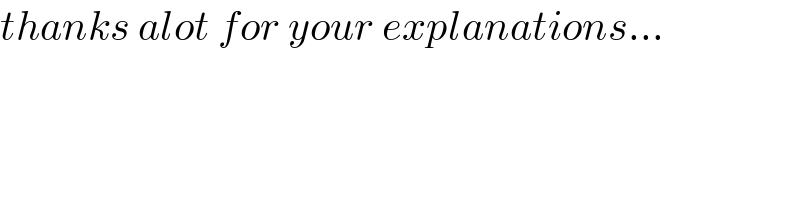
$${thanks}\:{alot}\:{for}\:{your}\:{explanations}... \\ $$
