
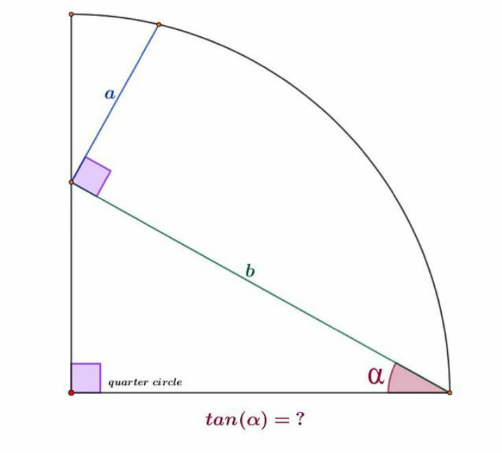
Question Number 143443 by mnjuly1970 last updated on 14/Jun/21
Commented by amin96 last updated on 14/Jun/21

$$? \\ $$$$ \\ $$
Answered by mr W last updated on 14/Jun/21
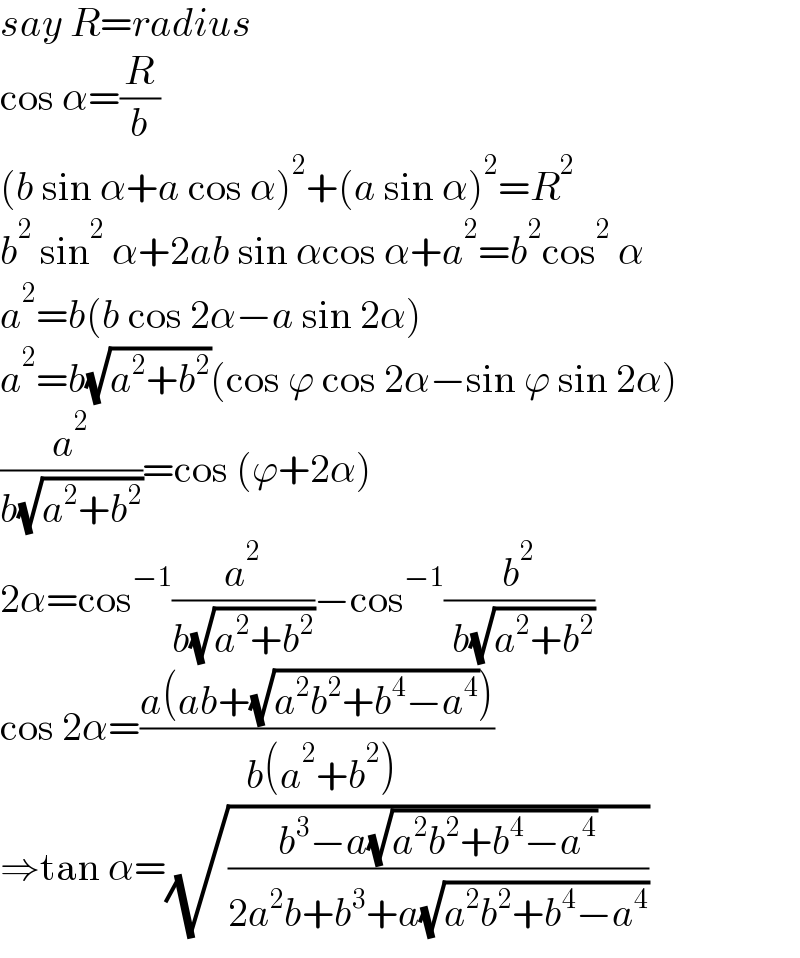
$${say}\:{R}={radius} \\ $$$$\mathrm{cos}\:\alpha=\frac{{R}}{{b}} \\ $$$$\left({b}\:\mathrm{sin}\:\alpha+{a}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\left({a}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\alpha+\mathrm{2}{ab}\:\mathrm{sin}\:\alpha\mathrm{cos}\:\alpha+{a}^{\mathrm{2}} ={b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$$${a}^{\mathrm{2}} ={b}\left({b}\:\mathrm{cos}\:\mathrm{2}\alpha−{a}\:\mathrm{sin}\:\mathrm{2}\alpha\right) \\ $$$${a}^{\mathrm{2}} ={b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left(\mathrm{cos}\:\varphi\:\mathrm{cos}\:\mathrm{2}\alpha−\mathrm{sin}\:\varphi\:\mathrm{sin}\:\mathrm{2}\alpha\right) \\ $$$$\frac{{a}^{\mathrm{2}} }{{b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}=\mathrm{cos}\:\left(\varphi+\mathrm{2}\alpha\right) \\ $$$$\mathrm{2}\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{{a}^{\mathrm{2}} }{{b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}−\mathrm{cos}^{−\mathrm{1}} \frac{{b}^{\mathrm{2}} }{\:{b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\frac{{a}\left({ab}+\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} −{a}^{\mathrm{4}} }\right)}{\:{b}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\sqrt{\frac{{b}^{\mathrm{3}} −{a}\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} −{a}^{\mathrm{4}} }}{\mathrm{2}{a}^{\mathrm{2}} {b}+{b}^{\mathrm{3}} +{a}\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} −{a}^{\mathrm{4}} }}} \\ $$
Commented by mnjuly1970 last updated on 14/Jun/21
$${thanks}\:{alot}\:{Mr}\:\:{W}.... \\ $$
