
Previous in Relation and Functions Next in Relation and Functions
Question Number 143258 by Mathspace last updated on 12/Jun/21
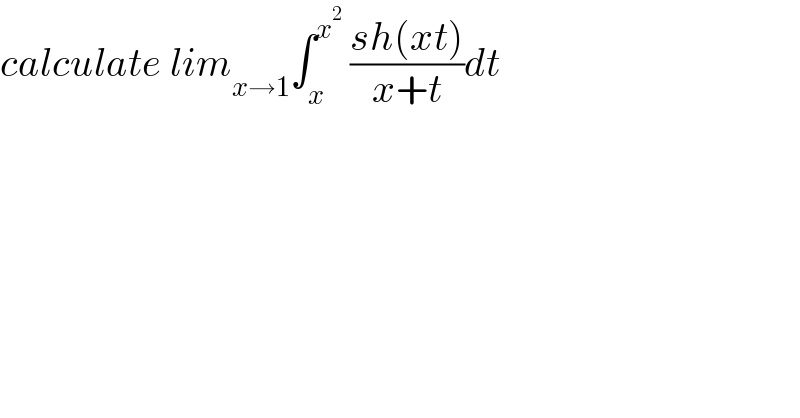
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{1}} \int_{{x}} ^{{x}^{\mathrm{2}} } \:\frac{{sh}\left({xt}\right)}{{x}+{t}}{dt} \\ $$
Answered by Mathspace last updated on 13/Jun/21
![∫_x ^x^2 ((sh(xt))/(x+t))dt =_(xt=u) ∫_x^2 ^x^3 ((sinu)/(x+(u/x)))(du/x) =∫_x^2 ^x^3 ((sinu)/(x^(2 ) +u))du =Y(x) ∃c∈]x^2 ,x^3 [ /Y(x)=sinc∫_x^2 ^x^3 (du/(u+x^2 )) =sinc[log∣u+x^2 ∣]_x^2 ^x^3 =sinc{log∣((x^3 +x^2 )/(x^2 +x^2 ))∣} sinclog∣((1+x)/2)∣ ⇒ lim_(x→1) Y(x)=sin(1)log(1)=0 ⇒ lim_(x→1) ∫_x ^x^2 ((sh(xt))/(x+t))dt=0](Q143385.png)
$$\int_{{x}} ^{{x}^{\mathrm{2}} } \:\frac{{sh}\left({xt}\right)}{{x}+{t}}{dt}\:=_{{xt}={u}} \:\:\int_{{x}^{\mathrm{2}} } ^{{x}^{\mathrm{3}} } \:\frac{{sinu}}{{x}+\frac{{u}}{{x}}}\frac{{du}}{{x}} \\ $$$$=\int_{{x}^{\mathrm{2}} } ^{{x}^{\mathrm{3}} } \:\frac{{sinu}}{{x}^{\mathrm{2}\:} +{u}}{du}\:={Y}\left({x}\right) \\ $$$$\left.\exists{c}\in\right]{x}^{\mathrm{2}} ,{x}^{\mathrm{3}} \left[\:\:/{Y}\left({x}\right)={sinc}\int_{{x}^{\mathrm{2}} } ^{{x}^{\mathrm{3}} } \:\frac{{du}}{{u}+{x}^{\mathrm{2}} }\right. \\ $$$$={sinc}\left[{log}\mid{u}+{x}^{\mathrm{2}} \mid\right]_{{x}^{\mathrm{2}} } ^{{x}^{\mathrm{3}} } \\ $$$$={sinc}\left\{{log}\mid\frac{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\mid\right\} \\ $$$${sinclog}\mid\frac{\mathrm{1}+{x}}{\mathrm{2}}\mid\:\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} {Y}\left({x}\right)={sin}\left(\mathrm{1}\right){log}\left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \int_{{x}} ^{{x}^{\mathrm{2}} } \:\frac{{sh}\left({xt}\right)}{{x}+{t}}{dt}=\mathrm{0} \\ $$
