
Question Number 141868 by mnjuly1970 last updated on 24/May/21
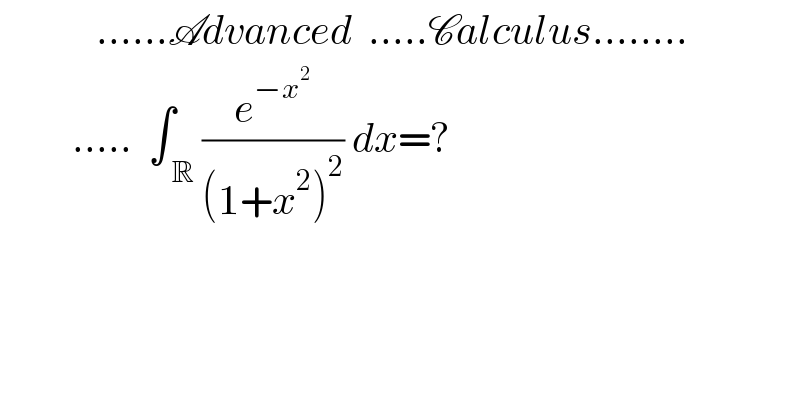
$$\:\:\:\:\:\:\:\:\:\:\:\:......\mathscr{A}{dvanced}\:\:.....\mathscr{C}{alculus}........ \\ $$$$\:\:\:\:\:\:\:\:\:.....\:\:\int_{\:\mathbb{R}} ^{\:} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}=? \\ $$$$\:\:\:\:\: \\ $$
Commented by mindispower last updated on 24/May/21
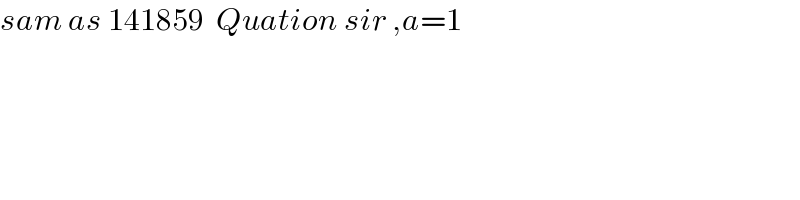
$${sam}\:{as}\:\mathrm{141859}\:\:{Quation}\:{sir}\:,{a}=\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 24/May/21
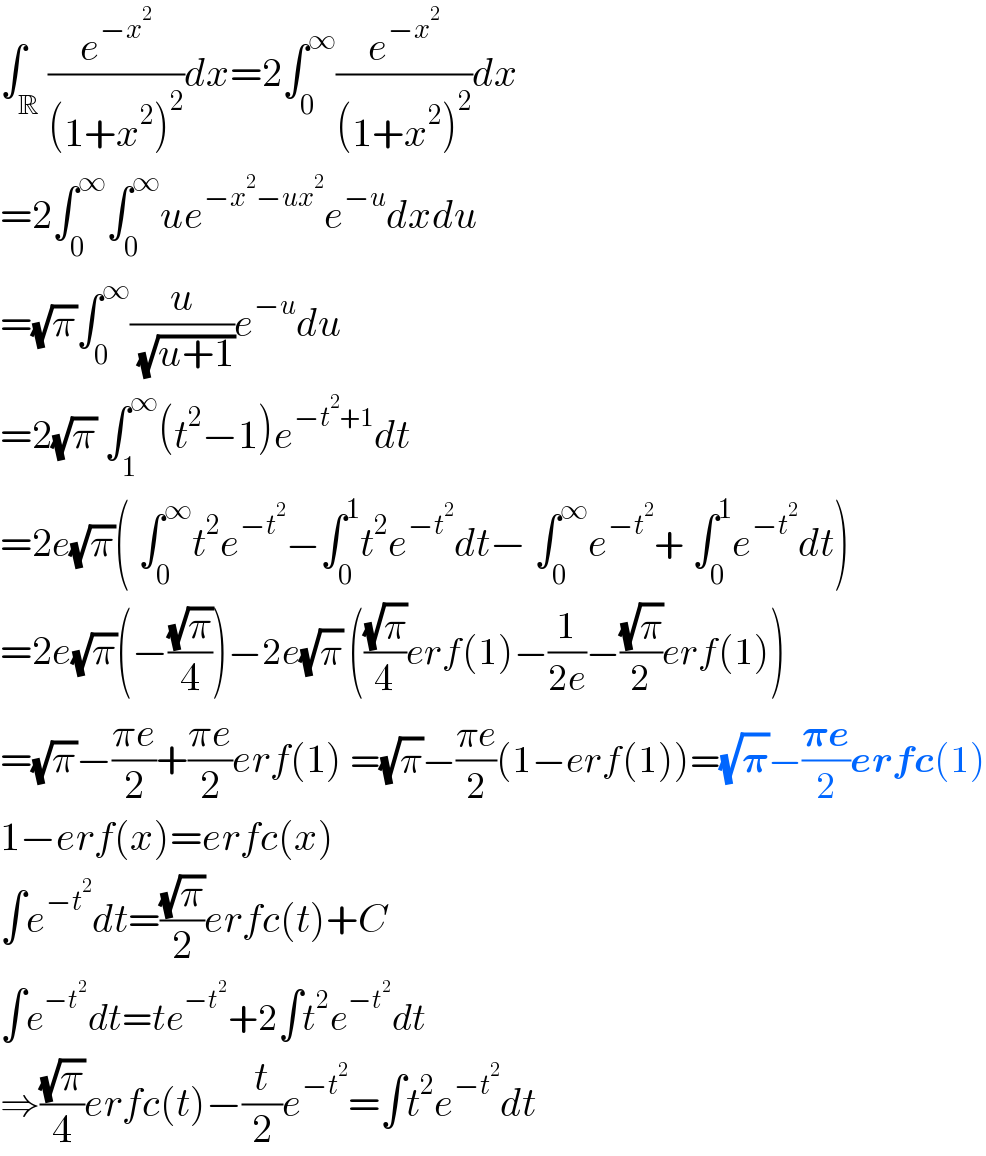
$$\int_{\mathbb{R}} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {ue}^{−{x}^{\mathrm{2}} −{ux}^{\mathrm{2}} } {e}^{−{u}} {dxdu} \\ $$$$=\sqrt{\pi}\int_{\mathrm{0}} ^{\infty} \frac{{u}}{\:\sqrt{{u}+\mathrm{1}}}{e}^{−{u}} {du} \\ $$$$=\mathrm{2}\sqrt{\pi}\:\int_{\mathrm{1}} ^{\infty} \left({t}^{\mathrm{2}} −\mathrm{1}\right){e}^{−{t}^{\mathrm{2}} +\mathrm{1}} {dt} \\ $$$$=\mathrm{2}{e}\sqrt{\pi}\left(\:\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{2}} {e}^{−{t}^{\mathrm{2}} } −\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} {e}^{−{t}^{\mathrm{2}} } {dt}−\:\int_{\mathrm{0}} ^{\infty} {e}^{−{t}^{\mathrm{2}} } +\:\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{t}^{\mathrm{2}} } {dt}\right) \\ $$$$=\mathrm{2}{e}\sqrt{\pi}\left(−\frac{\sqrt{\pi}}{\mathrm{4}}\right)−\mathrm{2}{e}\sqrt{\pi}\:\left(\frac{\sqrt{\pi}}{\mathrm{4}}{erf}\left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}{e}}−\frac{\sqrt{\pi}}{\mathrm{2}}{erf}\left(\mathrm{1}\right)\right) \\ $$$$=\sqrt{\pi}−\frac{\pi{e}}{\mathrm{2}}+\frac{\pi{e}}{\mathrm{2}}{erf}\left(\mathrm{1}\right)\:=\sqrt{\pi}−\frac{\pi{e}}{\mathrm{2}}\left(\mathrm{1}−{erf}\left(\mathrm{1}\right)\right)=\sqrt{\boldsymbol{\pi}}−\frac{\boldsymbol{\pi{e}}}{\mathrm{2}}\boldsymbol{{erfc}}\left(\mathrm{1}\right) \\ $$$$\mathrm{1}−{erf}\left({x}\right)={erfc}\left({x}\right) \\ $$$$\int{e}^{−{t}^{\mathrm{2}} } {dt}=\frac{\sqrt{\pi}}{\mathrm{2}}{erfc}\left({t}\right)+{C} \\ $$$$\int{e}^{−{t}^{\mathrm{2}} } {dt}={te}^{−{t}^{\mathrm{2}} } +\mathrm{2}\int{t}^{\mathrm{2}} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$\Rightarrow\frac{\sqrt{\pi}}{\mathrm{4}}{erfc}\left({t}\right)−\frac{{t}}{\mathrm{2}}{e}^{−{t}^{\mathrm{2}} } =\int{t}^{\mathrm{2}} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$
Commented by mathmax by abdo last updated on 24/May/21
![f(a)=∫_0 ^∞ (e^(−x^2 ) /(x^2 +a^2 ))dx ⇒f(a)=∫_0 ^∞ ∫_0 ^∞ (e^(−t(x^2 +a^2 )) dt)e^(−x^2 ) dx =∫_0 ^∞ ( ∫_0 ^∞ e^(−tx^2 −x^2 ) dx)e^(−ta^2 ) dt [but ∫_0 ^∞ e^(−tx^2 −x^2 ) dx =∫_0 ^∞ e^(−(t+1)x^2 ) dx =_((√(t+1))x=z) ∫_0 ^∞ e^(−z^2 ) (dz/( (√(t+1))))=((√π)/(2(√(t+1)))) ⇒ f(a)=((√π)/2)∫_0 ^∞ (e^(−ta^2 ) /( (√(t+1))))dt =_((√(t+1))=u) ((√π)/2)∫_1 ^∞ (e^(−a^2 (u^2 −1)) /u)(2u)du =(√π)e^a^2 ∫_1 ^∞ e^(−a^2 u^2 ) du ⇒ f^′ (a)=2a(√π)e^a^2 ∫_1 ^∞ e^(−a^2 u^2 ) du +(√π)e^a^2 ∫_1 ^∞ −2au^2 e^(−a^2 u^2 ) du =2a(√π)e^a^2 ∫_1 ^∞ e^(−a^2 u^2 ) du −2a(√π)e^a^2 ∫_1 ^∞ u^2 e^(−a^2 u^2 ) du [also ∫_1 ^∞ e^(−a^2 u^2 ) du =_(au=z) ∫_a ^∞ e^(−z^2 ) (dz/a) and ∫_1 ^∞ u^2 e^(−a^2 u^2 ) du =_(au=z) ∫_a ^∞ (z^2 /a^2 )e^(−z^2 ) (dz/a)=(1/a^3 )∫_a ^∞ z^2 e^(−z^2 ) dz ⇒ f^′ (a)=2(√π)e^a^2 ∫_a ^∞ e^(−z^2 ) dz−((2(√π))/a^2 ) e^a^2 ∫_a ^∞ z^2 e^(−z^2 ) dz f^′ (a)=−2a ∫_0 ^∞ (e^(−x^2 ) /((x^2 +a^2 )^2 ))dx ⇒ −2a ∫_0 ^∞ (e^(−x^2 ) /((x^2 +a^2 )^2 ))dx =2(√π)e^a^2 (∫_a ^∞ e^(−z^2 ) dz−(1/a^2 )∫_a ^∞ z^2 e^(−z^2 ) dz) ⇒ ∫_0 ^∞ (e^(−x^2 ) /((x^2 +a^2 )^2 ))dx =(√π)e^a^2 ((1/a^3 )∫_a ^∞ z^2 e^(−z^2 ) dz−∫_a ^∞ e^(−z^2 ) dz) a=(√3) ⇒∫_0 ^∞ (e^(−x^2 ) /((x^2 +3)^2 ))dx =(√π)e^3 ((1/(3(√3)))∫_(√3) ^∞ z^2 e^(−z^2 ) dz−∫_(√3) ^∞ e^(−z^2 ) dz) a=1 ⇒∫_0 ^∞ (e^(−x^2 ) /((x^2 +1)^2 ))dx=(√π)e(∫_1 ^∞ z^2 e^(−z^2 ) dz−∫_1 ^∞ e^(−z^2 ) dz) we have ∫_1 ^∞ z(ze^(−z^2 ) )dz =−(1/2)∫_1 ^∞ z(−2z e^(−z^2 ) )dz =−(1/2){ [ze^(−z^2 ) ]_1 ^∞ −∫_0 ^∞ ze^(−z^2 ) dz} =−(1/2){e^(−1) −[−(1/2)e^(−z^2 ) ]_1 ^∞ }=−(1/2)(e^(−1) −(1/2)e^(−1) ) =−(1/2)×(1/2)e^(−1) =−(1/(4e)) ....](Q141919.png)
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{e}^{−\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)} \mathrm{dt}\right)\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\right)\mathrm{e}^{−\mathrm{ta}^{\mathrm{2}} } \mathrm{dt}\:\left[\mathrm{but}\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{t}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=_{\sqrt{\mathrm{t}+\mathrm{1}}\mathrm{x}=\mathrm{z}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \frac{\mathrm{dz}}{\:\sqrt{\mathrm{t}+\mathrm{1}}}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{t}+\mathrm{1}}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{ta}^{\mathrm{2}} } }{\:\sqrt{\mathrm{t}+\mathrm{1}}}\mathrm{dt}\:=_{\sqrt{\mathrm{t}+\mathrm{1}}=\mathrm{u}} \:\:\frac{\sqrt{\pi}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)} }{\mathrm{u}}\left(\mathrm{2u}\right)\mathrm{du} \\ $$$$=\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \:\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} } \mathrm{du}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\mathrm{2a}\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \:\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} } \mathrm{du}\:+\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \int_{\mathrm{1}} ^{\infty} −\mathrm{2au}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} } \:\mathrm{du} \\ $$$$=\mathrm{2a}\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \:\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} } \mathrm{du}\:−\mathrm{2a}\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \int_{\mathrm{1}} ^{\infty} \:\mathrm{u}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} } \mathrm{du}\:\left[\mathrm{also}\right. \\ $$$$\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} } \mathrm{du}\:=_{\mathrm{au}=\mathrm{z}} \:\:\int_{\mathrm{a}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \frac{\mathrm{dz}}{\mathrm{a}}\:\:\mathrm{and} \\ $$$$\int_{\mathrm{1}} ^{\infty} \:\mathrm{u}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} } \mathrm{du}\:=_{\mathrm{au}=\mathrm{z}} \:\:\int_{\mathrm{a}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \frac{\mathrm{dz}}{\mathrm{a}}=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }\int_{\mathrm{a}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\mathrm{2}\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \int_{\mathrm{a}} ^{\infty} \mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}−\frac{\mathrm{2}\sqrt{\pi}}{\mathrm{a}^{\mathrm{2}} }\:\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \int_{\mathrm{a}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\mathrm{2a}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$−\mathrm{2a}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{2}\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \left(\int_{\mathrm{a}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{a}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }\int_{\mathrm{a}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}−\int_{\mathrm{a}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\right) \\ $$$$\mathrm{a}=\sqrt{\mathrm{3}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\mathrm{dx}\:=\sqrt{\pi}\mathrm{e}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}}\int_{\sqrt{\mathrm{3}}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}−\int_{\sqrt{\mathrm{3}}} ^{\infty} \mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\right) \\ $$$$\mathrm{a}=\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\sqrt{\pi}\mathrm{e}\left(\int_{\mathrm{1}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}−\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{1}} ^{\infty} \:\mathrm{z}\left(\mathrm{ze}^{−\mathrm{z}^{\mathrm{2}} } \right)\mathrm{dz}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \mathrm{z}\left(−\mathrm{2z}\:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \right)\mathrm{dz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left[\mathrm{ze}^{−\mathrm{z}^{\mathrm{2}} } \right]_{\mathrm{1}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} \mathrm{ze}^{−\mathrm{z}^{\mathrm{2}} } \:\mathrm{dz}\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{e}^{−\mathrm{1}} −\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \right]_{\mathrm{1}} ^{\infty} \right\}=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{e}^{−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{1}} \right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{4e}}\:.... \\ $$
Commented by mathmax by abdo last updated on 24/May/21
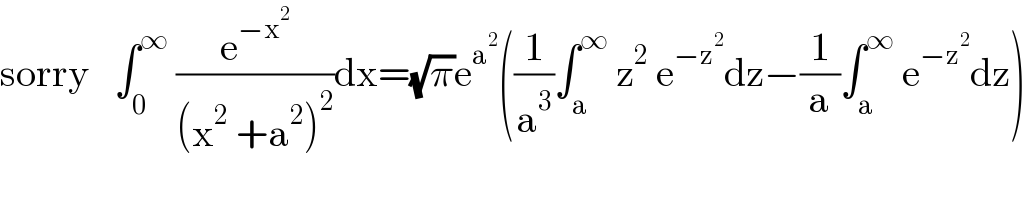
$$\mathrm{sorry}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\sqrt{\pi}\mathrm{e}^{\mathrm{a}^{\mathrm{2}} } \left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }\int_{\mathrm{a}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}−\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{a}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\right) \\ $$
